What Is 15 Percent Of 30
Greels
Mar 30, 2025 · 5 min read
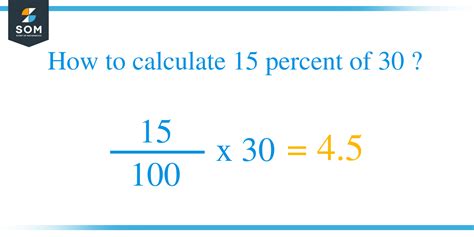
Table of Contents
What is 15 Percent of 30? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 15 percent of 30?" opens a door to a vast world of mathematical concepts and their practical applications across various fields. While the answer itself is straightforward (4.5), understanding the underlying principles and the diverse contexts in which percentage calculations are used is crucial. This article will explore the calculation, delve into the meaning of percentages, and illustrate their importance in everyday life, business, and advanced mathematics.
Calculating 15 Percent of 30: The Basics
The most fundamental way to calculate 15% of 30 is to translate the percentage into a decimal and then multiply. Remember that a percentage is simply a fraction out of 100. Therefore, 15% can be written as 15/100 or 0.15.
The calculation is as follows:
0.15 * 30 = 4.5
Therefore, 15 percent of 30 is 4.5.
Understanding Percentages: Beyond the Calculation
Percentages are a powerful tool for representing proportions and ratios. They provide a standardized way to compare different quantities, making them incredibly useful across a wide range of disciplines. Understanding their fundamental nature is key to mastering their application.
-
Percentages as Fractions: As mentioned earlier, a percentage is a fraction with a denominator of 100. This means that 25% is equivalent to 25/100, which simplifies to 1/4. Understanding this equivalence is critical for simplifying calculations and making comparisons.
-
Percentages as Decimals: Expressing percentages as decimals (e.g., 15% as 0.15) simplifies calculations, especially when using calculators or computer programs. Converting between percentages and decimals is a fundamental skill for anyone working with numerical data.
-
The Importance of Context: The meaning of a percentage is heavily dependent on the context in which it is used. For example, a 15% increase in sales is very different from a 15% decrease in profits. Understanding the context is crucial for accurate interpretation and decision-making.
Real-World Applications of Percentage Calculations
The application of percentage calculations permeates almost every aspect of modern life. Here are some examples:
1. Finance and Business:
-
Interest Rates: Banks and financial institutions use percentages extensively to calculate interest on loans, savings accounts, and investments. Understanding interest rates is crucial for making informed financial decisions. For example, calculating the interest accrued on a loan or the return on an investment often involves percentage calculations.
-
Sales Tax: Sales tax is a percentage of the price of goods and services. Calculating the final price of an item often requires adding the sales tax percentage to the original price.
-
Discounts and Markups: Businesses use percentages to offer discounts on products (e.g., a 20% off sale) or to mark up the prices of goods to ensure profitability.
-
Profit Margins: Businesses use percentages to calculate their profit margins, which represent the percentage of revenue remaining after deducting costs.
-
Investment Returns: The return on investments is often expressed as a percentage, enabling investors to compare the performance of different investment options.
2. Science and Statistics:
-
Data Analysis: Percentages are frequently used in data analysis and statistics to represent proportions and frequencies within datasets. For example, researchers might report the percentage of participants in a study who showed a particular outcome.
-
Probability: Probability calculations often involve percentages, representing the likelihood of certain events occurring.
-
Scientific Measurements: Percentages are used in various scientific measurements, such as calculating the concentration of a solution or the percentage error in an experiment.
3. Everyday Life:
-
Tipping: Calculating a tip at a restaurant often involves calculating a percentage of the bill.
-
Sales and Promotions: Understanding percentages helps consumers take advantage of sales and promotional offers.
-
Nutrition Labels: Food labels often list the percentage of daily recommended values for different nutrients.
-
Household Budgeting: Individuals often budget their expenses as percentages of their income.
Advanced Percentage Calculations and Concepts
Beyond the simple calculation of 15% of 30, there are more advanced percentage calculations and related concepts to consider:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%.
-
Finding the Original Value: If you know the final value after a percentage increase or decrease, you can work backward to find the original value. This often involves using algebraic equations.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and the accumulated interest. This concept is critical in finance and investment calculations.
-
Percentage Points: It's important to differentiate between percentage points and percentage changes. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Solving More Complex Percentage Problems
Let's consider some more complex examples that showcase the versatility of percentage calculations:
Example 1: A shirt costs $30. It's on sale for 15% off. What is the sale price?
First, calculate the discount: 0.15 * $30 = $4.50
Then, subtract the discount from the original price: $30 - $4.50 = $25.50
The sale price of the shirt is $25.50.
Example 2: John invested $1000, and his investment increased by 20% in the first year and decreased by 10% in the second year. What is the final value of his investment?
Year 1: $1000 * 0.20 = $200 increase; $1000 + $200 = $1200
Year 2: $1200 * 0.10 = $120 decrease; $1200 - $120 = $1080
The final value of John's investment is $1080. Note that this illustrates the non-linearity of percentage changes.
Example 3: A store sold 150 items. 20% of the items were defective. How many items were not defective?
Number of defective items: 0.20 * 150 = 30
Number of non-defective items: 150 - 30 = 120
There were 120 non-defective items.
Conclusion: The Ubiquity of Percentages
The seemingly simple question of "What is 15 percent of 30?" provides a springboard to explore the multifaceted nature of percentages and their crucial role in numerous contexts. From simple everyday calculations to complex financial modeling and scientific analysis, percentages offer a standardized and efficient way to represent proportions, enabling effective communication and informed decision-making across various disciplines. Mastering percentage calculations is a fundamental skill that enhances understanding in numerous fields and empowers individuals to navigate the complexities of the numerical world.
Latest Posts
Latest Posts
-
Matrix Multiplication Step By Step Calculator
Apr 01, 2025
-
10 Is What Percent Of 70
Apr 01, 2025
-
81 Kg Is How Many Pounds
Apr 01, 2025
-
What Is 191 Cm In Feet
Apr 01, 2025
-
Equations Of Parallel And Perpendicular Lines Calculator
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
