Slope Parallel And Perpendicular Lines Calculator
Greels
Mar 28, 2025 · 5 min read
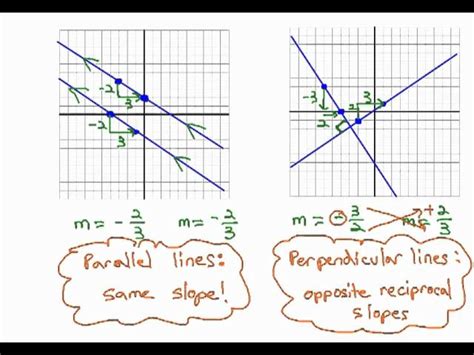
Table of Contents
Slope Parallel and Perpendicular Lines Calculator: A Comprehensive Guide
Understanding slopes and their relationships is fundamental in geometry and various applications. This comprehensive guide explores parallel and perpendicular lines, their slopes, and how to utilize a slope parallel and perpendicular lines calculator effectively. We'll delve into the underlying mathematical principles and provide practical examples to solidify your understanding.
What are Parallel and Perpendicular Lines?
Before diving into calculations, let's define our key terms:
-
Parallel Lines: These are lines that lie in the same plane and never intersect, no matter how far they are extended. They maintain a constant distance from each other. A critical property is that parallel lines have the same slope.
-
Perpendicular Lines: These lines intersect at a right angle (90 degrees). The relationship between their slopes is crucial: the slope of one line is the negative reciprocal of the slope of the other.
Understanding Slope
The slope (often represented as 'm') of a line describes its steepness. It's the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line. The formula for calculating the slope given two points (x1, y1) and (x2, y2) is:
m = (y2 - y1) / (x2 - x1)
A positive slope indicates a line that rises from left to right, while a negative slope indicates a line that falls from left to right. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
Calculating Slopes for Parallel and Perpendicular Lines
Let's examine how to determine the slopes of parallel and perpendicular lines:
1. Parallel Lines:
If two lines are parallel, they share the same slope. If you know the slope of one line, you automatically know the slope of its parallel counterpart.
Example: If line A has a slope of 2, any line parallel to line A will also have a slope of 2.
2. Perpendicular Lines:
For perpendicular lines, the relationship is more nuanced. The slope of one line is the negative reciprocal of the slope of the other line. To find the negative reciprocal:
- Invert the fraction: If the slope is a fraction (e.g., 3/4), flip it (4/3). If it's a whole number, express it as a fraction (e.g., 2 becomes 2/1).
- Change the sign: If the slope is positive, make it negative, and vice-versa.
Example: If line B has a slope of 3/4, a line perpendicular to line B will have a slope of -4/3. If line C has a slope of -2, a perpendicular line will have a slope of 1/2.
Using a Slope Parallel and Perpendicular Lines Calculator
A slope parallel and perpendicular lines calculator streamlines these calculations. These tools typically require you to input the coordinates of two points for each line. The calculator then:
- Calculates the slope of each line using the formula mentioned earlier.
- Determines if the lines are parallel or perpendicular based on the relationship between their slopes.
- Provides the slopes of parallel and perpendicular lines for each inputted line. This is particularly useful if you're working with an existing line and need to find the slope of a line parallel or perpendicular to it.
Practical Applications
The concept of parallel and perpendicular lines, and their slopes, has widespread applications in various fields:
-
Engineering: Designing structures, bridges, and roads requires precise calculations involving parallel and perpendicular lines to ensure stability and functionality.
-
Architecture: Architectural designs rely heavily on these concepts for creating aesthetically pleasing and structurally sound buildings. Parallel and perpendicular lines contribute to symmetry and balance in design.
-
Computer Graphics: In computer-aided design (CAD) and game development, representing objects and their movements accurately requires understanding how to manipulate lines and their slopes.
-
Physics: Many physics concepts, such as vectors and forces, utilize the principles of parallel and perpendicular lines.
-
Cartography: Creating maps and determining distances and directions often involve calculations related to slopes and angles of lines.
Beyond Basic Calculations: Advanced Concepts
While a calculator simplifies the process, a deeper understanding of the underlying mathematics is crucial for complex problems. Here are some advanced concepts related to slopes and lines:
-
Lines with Undefined Slope: Vertical lines have an undefined slope because the change in x (run) is zero, resulting in division by zero, which is undefined in mathematics.
-
Lines with Zero Slope: Horizontal lines have a slope of zero because the change in y (rise) is zero.
-
Equation of a Line: The slope-intercept form of a line's equation is
y = mx + b, where 'm' is the slope and 'b' is the y-intercept (the point where the line intersects the y-axis). The point-slope form isy - y1 = m(x - x1), where (x1, y1) is a point on the line.
Troubleshooting and Common Mistakes
When working with slopes, some common mistakes can arise:
-
Incorrectly applying the slope formula: Pay close attention to the order of subtraction in the numerator and denominator of the slope formula.
-
Misinterpreting negative reciprocals: Remember to both invert the fraction and change the sign when calculating the negative reciprocal for perpendicular lines.
-
Confusing parallel and perpendicular relationships: Clearly understand the difference between the conditions for parallel (same slope) and perpendicular (negative reciprocal slopes) lines.
Improving Your Skills
To improve your understanding and proficiency with slope calculations and the relationships between parallel and perpendicular lines, consider these strategies:
-
Practice: Work through numerous examples and problems involving different types of lines and slopes.
-
Visual Aids: Use graphs to visualize lines and their slopes, which can greatly improve your understanding.
-
Real-World Applications: Seek out real-world applications of these concepts to see how they are utilized in practice.
-
Online Resources: Explore additional online resources, tutorials, and interactive tools to reinforce your knowledge.
Conclusion
A thorough grasp of parallel and perpendicular lines and their slopes is fundamental to many areas of mathematics and its applications. While a slope parallel and perpendicular lines calculator provides a convenient tool for calculations, a deeper understanding of the underlying principles is essential for solving more complex problems and appreciating the wide-ranging utility of this mathematical concept. By mastering these principles and utilizing the available tools effectively, you can confidently tackle various challenges involving lines and slopes. Remember to practice regularly and utilize available resources to further enhance your skills in this essential area of mathematics.
Latest Posts
Latest Posts
-
96 Mm Is How Many Inches
Mar 31, 2025
-
12 3 Y 5 2y 8
Mar 31, 2025
-
How Many Feet Is 500 Inches
Mar 31, 2025
-
How Much Is 113 Lbs In Kg
Mar 31, 2025
-
Cuanto Es 168 Libras En Kilos
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Slope Parallel And Perpendicular Lines Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
