Integral Of E To The Xy
Greels
Mar 28, 2025 · 5 min read
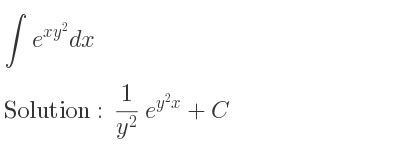
Table of Contents
The Integral of e^(xy): A Comprehensive Guide
The integral of e^(xy) is a deceptively simple-looking expression that leads to surprisingly diverse applications and solution methods. This comprehensive guide will delve into the intricacies of integrating e^(xy), exploring various scenarios, techniques, and their practical implications. We'll move from the simplest cases to more complex ones, equipping you with a thorough understanding of this essential mathematical concept.
Understanding the Problem: Why is ∫e^(xy)dy so Challenging?
Unlike the straightforward integration of e^x (which simply results in e^x + C), integrating e^(xy) with respect to y (or x) presents a unique challenge. The presence of two variables means the integration isn't as straightforward. The solution hinges on the context: are x and y independent variables? Is one a constant relative to the other? The answer determines the appropriate integration technique.
Case 1: x is a Constant
This is the most basic scenario. If x is treated as a constant during integration with respect to y, the solution becomes remarkably simple. We can apply the standard rule for integrating exponential functions:
∫e^(xy) dy = (1/x)e^(xy) + C (where x ≠ 0 and C is the constant of integration)
Explanation: We treat x as a constant multiplier. The derivative of xy with respect to y is simply x. The integral therefore follows the pattern ∫e^(kx) dx = (1/k)e^(kx) + C, where k is a constant.
Example: Find the integral of e^(3y) with respect to y.
Here, x is essentially 3 (a constant). Applying the formula:
∫e^(3y) dy = (1/3)e^(3y) + C
This clarifies that if one variable can be treated as a constant, integration is direct.
Case 2: x and y are Independent Variables – Double Integrals
When both x and y are independent variables, we move to the realm of double integrals. The integration process requires specifying limits of integration for both variables. The order of integration matters, and the solution involves iterative integration.
The General Form:
∬e^(xy) dA (where dA represents the area element, typically dxdy or dydx)
Example: Evaluate the double integral ∬e^(xy) dA over the region R defined by 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1.
We can choose to integrate with respect to x first or y first. Let's choose to integrate with respect to y first:
- Inner Integral (with respect to y):
∫₀¹ e^(xy) dy = [(1/x)e^(xy)]₀¹ = (1/x)(e^x - 1)
- Outer Integral (with respect to x):
∫₀¹ (1/x)(e^x - 1) dx
This integral is non-elementary, meaning it doesn't have a closed-form solution in terms of elementary functions. We'd need to resort to numerical methods (such as Simpson's rule or trapezoidal rule) or series expansions to approximate the value.
This example demonstrates the complexity that arises when dealing with independent variables and the limitations of finding explicit analytical solutions.
Case 3: x and y are Related – Change of Variables
If x and y are related through a specific function or equation, we might employ a change of variables to simplify the integral. This technique involves substituting new variables (u and v, for example) that lead to a more manageable integral. The Jacobian determinant plays a crucial role in handling the transformation of the area element.
Example (Illustrative): Consider a scenario where x and y are related by x = y². The integral would become ∫e^(y³) dy. Even with this substitution, the resulting integral may still not have an elementary solution. However, the change of variables approach might simplify the process or lead to a recognizable integral form in some instances.
Case 4: Using Series Expansions
When an explicit analytical solution is elusive, resorting to series expansions offers a viable path. The Taylor series expansion for e^u is:
e^u = 1 + u + u²/2! + u³/3! + ...
We can substitute xy for u:
e^(xy) = 1 + xy + (xy)²/2! + (xy)³/3! + ...
Integrating term by term, we get an infinite series representing the integral. This approach provides an approximate solution, the accuracy of which depends on the number of terms included in the series.
Applications of the Integral of e^(xy)
The integral of e^(xy), despite its integration challenges, finds applications in diverse fields:
-
Probability and Statistics: The bivariate normal distribution, a crucial concept in multivariate statistical analysis, involves integrals of exponential functions with multiple variables, often including variations of e^(xy) terms within the probability density function.
-
Quantum Mechanics: Solving the Schrödinger equation for certain quantum systems may involve integrals resembling ∫e^(xy) dy in their mathematical formulations.
-
Signal Processing and Image Analysis: Fourier transforms, vital for signal processing and image analysis, frequently involve integral transformations that might include similar exponential terms.
-
Partial Differential Equations (PDEs): Solving specific types of PDEs, like those related to heat transfer or diffusion, might involve integrals containing expressions closely related to e^(xy).
Numerical Methods for Approximation
As demonstrated earlier, many integrals involving e^(xy) do not yield elementary solutions. In these cases, numerical integration techniques become indispensable. Here are some prominent methods:
-
Trapezoidal Rule: This method approximates the integral using trapezoids to represent the area under the curve.
-
Simpson's Rule: This method enhances accuracy by using parabolic arcs to represent the area under the curve.
-
Gaussian Quadrature: This sophisticated technique utilizes strategically chosen points and weights for more precise approximation.
Numerical methods offer a practical solution when dealing with integrals that defy analytical solutions. The choice of method depends on the desired level of accuracy and computational resources.
Conclusion: Navigating the Intricacies of ∫e^(xy)dy
The integral of e^(xy) serves as a powerful illustration of how simple-looking mathematical expressions can lead to unexpectedly intricate integration problems. Understanding the context—whether x is a constant, x and y are independent, or they're related—is paramount in choosing the appropriate approach. While simple cases allow for direct integration, more complex situations often require double integrals, change of variables, series expansions, or numerical approximation techniques. Mastery of these methods is crucial for tackling problems in numerous scientific and engineering disciplines. This guide provides a foundation for navigating these complexities and effectively solving integrals involving e^(xy) in diverse contexts. Remember, the key to success lies in careful consideration of the problem's specifics and choosing the most suitable integration technique to achieve a solution, whether analytical or approximate.
Latest Posts
Latest Posts
-
72 Inches Is How Many Centimeters
Mar 31, 2025
-
96 Mm Is How Many Inches
Mar 31, 2025
-
12 3 Y 5 2y 8
Mar 31, 2025
-
How Many Feet Is 500 Inches
Mar 31, 2025
-
How Much Is 113 Lbs In Kg
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Integral Of E To The Xy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
