Y 2y Y 2 24e X 40e 5x
Greels
Apr 01, 2025 · 4 min read
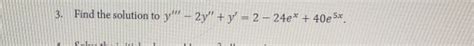
Table of Contents
Deconstructing the Equation: Exploring the Mathematical Landscape of "y 2y y 2 24e x 40e 5x"
This seemingly simple string of characters, "y 2y y 2 24e x 40e 5x," presents a fascinating challenge. At first glance, it appears to be a jumbled collection of variables and constants. However, a closer examination reveals a potential mathematical relationship ripe for exploration. This article will delve into the possible interpretations of this expression, investigating its structure, potential solutions, and the broader mathematical concepts it touches upon. We will explore different approaches to understanding and solving this enigmatic equation, catering to different levels of mathematical expertise.
Understanding the Components:
Before attempting to solve or interpret the equation, let's break down its constituent parts. We have:
- Variables:
yandxare likely representing unknown variables. Their relationship is the core of the problem. - Constants: The numbers
2,24,40, and5are constants. They represent fixed values. - Exponential Term: The presence of
esuggests the involvement of the exponential function (e^x), a fundamental concept in calculus and many areas of science.
Possible Interpretations and Approaches:
The absence of explicit operators between some terms introduces ambiguity. We can explore different interpretations to resolve this uncertainty:
1. Interpreting as a System of Equations:
One plausible interpretation is that the expression represents a system of equations. We could separate it into two distinct equations:
- Equation 1:
y + 2y + y = 24e - Equation 2:
x + 40e = 5x
Let's solve each equation individually:
Solving Equation 1:
y + 2y + y = 24e simplifies to 4y = 24e. Dividing both sides by 4, we get y = 6e.
Solving Equation 2:
x + 40e = 5x can be rearranged as 40e = 4x. Dividing both sides by 4, we obtain x = 10e.
Therefore, under this interpretation, the solution is y = 6e and x = 10e. This highlights a direct proportional relationship between x and y, where x = (5/3)y.
2. Interpreting as a Single, Implicit Equation:
Alternatively, we might interpret the expression as a single, implicit equation, where the relationship between x and y is not explicitly defined. This could look something like this:
4y + 24e - 40e = 5x
Simplifying:
4y - 16e = 5x
This equation represents a linear relationship between x and y. We can express it in slope-intercept form:
y = (5/4)x + 4e
This interpretation suggests that for any given value of x, we can find a corresponding value for y. The graph of this equation would be a straight line with a slope of 5/4 and a y-intercept of 4e.
3. Exploring Exponential Relationships:
The presence of e might imply more complex exponential relationships. Perhaps the expression represents a system of differential equations or involves concepts like exponential growth or decay. For instance, the equation might represent a system where:
- The rate of change of
yis proportional toyitself (like in population growth models). - The rate of change of
xis related to the value ofy.
To explore these possibilities, we'd need additional context or information regarding the underlying processes that generated this equation. This interpretation calls for advanced mathematical tools and a deeper understanding of differential equations.
4. Considering Errors or Missing Information:
It's also essential to consider the possibility of errors or missing information in the original expression. The lack of clear operators makes it challenging to provide a definitive interpretation. Additional information about the context in which this expression appears would significantly aid in the analysis.
Broader Mathematical Concepts:
This seemingly simple expression opens doors to numerous mathematical concepts:
- Linear Algebra: The system-of-equations interpretation leads to concepts like linear dependence and independence, solution spaces, and matrix representations.
- Calculus: The presence of
enaturally brings in calculus, including concepts like differentiation, integration, and differential equations. - Numerical Methods: If the equation proved too complex for analytical solutions, numerical methods (approximation techniques) could be employed to find approximate solutions.
- Graph Theory: The visualization of the relationship between
xandycould involve graph theory concepts, particularly if the equation represents a network or system of interconnected variables.
Conclusion:
The expression "y 2y y 2 24e x 40e 5x" presents a fascinating case study in mathematical interpretation. While the absence of clear operators introduces ambiguity, we've explored multiple interpretations, highlighting the various mathematical tools and concepts involved. The simplest interpretations lead to straightforward linear relationships between x and y. However, the presence of the exponential constant e suggests the possibility of more intricate, potentially dynamic systems that would require a deeper mathematical analysis. The key takeaway is that a seemingly simple equation can open up a wide range of possibilities and invite exploration across different mathematical disciplines. The true meaning and solution depend heavily on the context from which this expression originated. Further information or clarification of the expression is needed to provide a conclusive and definitive solution. This exercise serves as a great example of the importance of clear notation and context in mathematical problems.
Latest Posts
Latest Posts
-
What Is 185 Pounds In Kilograms
Apr 02, 2025
-
300 Pounds Is How Many Kilograms
Apr 02, 2025
-
How Many Feet Are 30 Inches
Apr 02, 2025
-
How Many Inches Is 44 Centimeters
Apr 02, 2025
-
How Many Inches Is 49 Mm
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Y 2y Y 2 24e X 40e 5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
