X 3 7x 12 2 3
Greels
Apr 15, 2025 · 5 min read
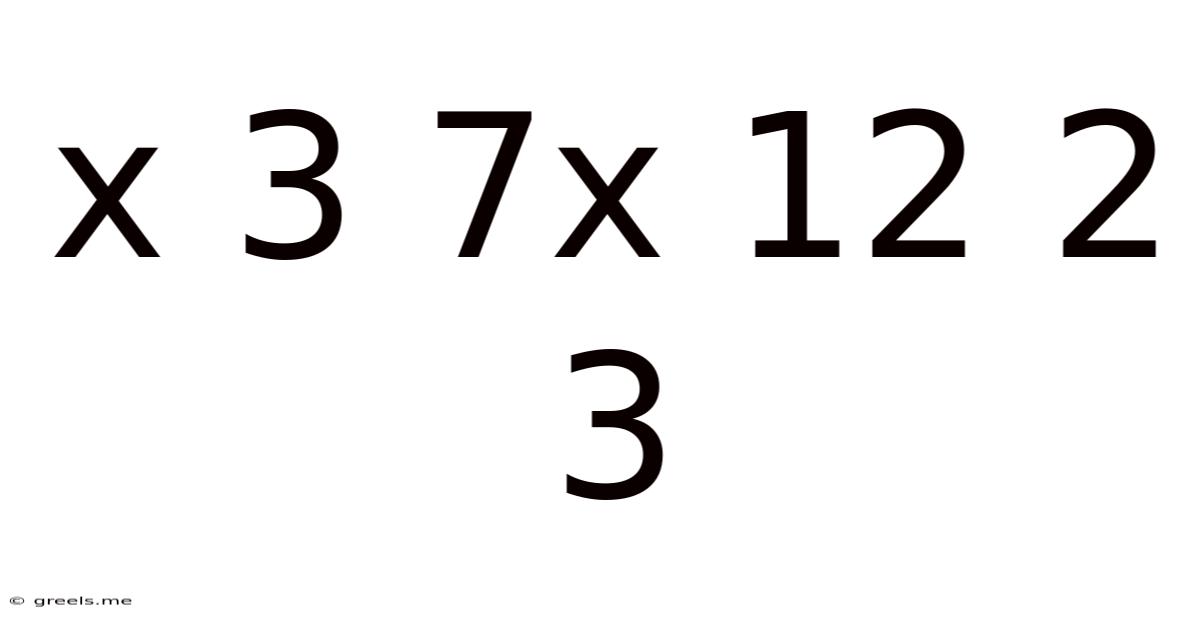
Table of Contents
Decoding the Mystery: Exploring the Mathematical Sequence x³ + 7x² + 12x + 2/3
The seemingly simple sequence "x³ + 7x² + 12x + 2/3" presents a fascinating challenge for mathematical exploration. While it might appear straightforward at first glance, delving into its properties reveals a rich tapestry of mathematical concepts, from basic algebra to more advanced polynomial analysis. This article aims to unravel the mysteries surrounding this sequence, exploring its characteristics, potential applications, and its place within the broader context of mathematics.
Understanding the Polynomial Expression
The core of our exploration is the cubic polynomial expression: x³ + 7x² + 12x + 2/3. This is a polynomial of degree three, meaning the highest power of the variable 'x' is 3. Polynomials are fundamental building blocks in algebra, and understanding their behavior is crucial in various mathematical fields.
Key Components:
- Coefficients: The numbers multiplying the powers of x (1, 7, 12, and 2/3) are called coefficients. They determine the shape and characteristics of the polynomial's graph.
- Variables: The 'x' represents a variable, which can take on different numerical values. The value of the expression changes depending on the value assigned to x.
- Constants: The constant term is 2/3. This is the value of the expression when x = 0.
- Degree: The degree of the polynomial is 3, the highest power of x. This indicates the maximum number of real roots (solutions where the expression equals zero) the polynomial can have.
Analyzing the Polynomial's Behavior
To fully understand the sequence, we need to analyze its behavior across different values of x. We can achieve this through several methods:
1. Graphing the Polynomial: Graphing the polynomial provides a visual representation of its behavior. Plotting points by substituting various x-values and calculating the corresponding y-values (the value of the polynomial) will reveal the curve's shape. The graph will show us:
- Roots (x-intercepts): The points where the graph intersects the x-axis (y=0). These are the solutions to the equation x³ + 7x² + 12x + 2/3 = 0. Finding these roots can be challenging and may require numerical methods or advanced algebraic techniques.
- Turning Points: The points where the curve changes direction (from increasing to decreasing or vice versa). A cubic polynomial can have up to two turning points.
- Overall Trend: The general behavior of the curve, whether it increases or decreases as x increases or decreases.
2. Calculating Derivatives: The first derivative of the polynomial reveals its slope at any given point, indicating whether the function is increasing or decreasing at that point. The second derivative helps identify concavity (whether the curve is concave up or concave down).
- First Derivative: The first derivative of x³ + 7x² + 12x + 2/3 is 3x² + 14x + 12. Setting this to zero and solving for x will give the x-coordinates of the turning points.
- Second Derivative: The second derivative is 6x + 14. This helps to determine the concavity of the curve at different points.
3. Investigating the Roots: Finding the roots (zeros) of the polynomial – the values of x that make the expression equal to zero – is a significant aspect of the analysis. This often requires numerical methods, such as the Newton-Raphson method, or approximation techniques since analytical solutions might be complex or impossible to obtain for higher-degree polynomials.
Potential Applications
The polynomial x³ + 7x² + 12x + 2/3, while seemingly abstract, has potential applications in several fields:
-
Modeling Real-world Phenomena: Polynomials are frequently used to model various real-world phenomena, particularly in fields like physics and engineering. This specific polynomial could potentially represent the trajectory of an object, the growth of a population, or other processes that exhibit cubic behavior.
-
Curve Fitting: In data analysis, polynomials are used to fit curves to sets of data points. This polynomial could be used to model data that shows a cubic trend.
-
Numerical Analysis: The study of the polynomial’s roots and behavior is crucial in numerical analysis, where algorithms are developed for approximating solutions to complex equations.
-
Calculus and Differential Equations: Polynomials are essential in calculus and differential equations. This specific polynomial might be a component within a larger system of equations or used for approximating solutions.
Expanding the Exploration: Related Concepts
Understanding this polynomial opens the door to exploring related mathematical concepts:
-
Polynomial Division: The polynomial could be divided by other polynomials to find factors and simplify the expression.
-
Partial Fraction Decomposition: If the polynomial were part of a rational function (a fraction with polynomials in the numerator and denominator), partial fraction decomposition would be a useful technique for simplification.
-
Taylor and Maclaurin Series: These series represent functions as infinite sums of polynomials, often used to approximate complex functions. The given polynomial might be a segment of a larger Taylor or Maclaurin series expansion of a more intricate function.
Advanced Mathematical Considerations
For those interested in pursuing more advanced aspects, several avenues of investigation exist:
-
Complex Roots: Polynomials of degree three can have up to three roots, some of which might be complex numbers (numbers involving the imaginary unit 'i'). Investigating these complex roots could reveal further insights into the polynomial's behavior.
-
Modular Arithmetic: Exploring the polynomial's behavior within different modular arithmetic systems (where calculations are done modulo a specific number) could unearth interesting properties and patterns.
-
Abstract Algebra: The polynomial could be examined within the context of abstract algebra, where concepts like rings and fields provide a more general framework for studying polynomial expressions.
Conclusion: A Deep Dive into a Simple Sequence
The seemingly simple sequence x³ + 7x² + 12x + 2/3 provides a gateway to a rich and diverse landscape within the realm of mathematics. Through careful analysis, graphing, and the application of various mathematical techniques, we can uncover its hidden properties, explore its potential applications, and appreciate its role within the broader tapestry of mathematical thought. This exploration highlights the power of seemingly simple mathematical expressions to unlock profound insights and connections within the world of numbers. The journey of understanding this polynomial serves as a microcosm of the broader mathematical enterprise – a continuous process of exploration, discovery, and the pursuit of deeper understanding. Further research and exploration into its properties will undoubtedly reveal even more hidden facets of this captivating mathematical sequence.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 7x 12 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.