X 2 Y 2 Z 2 4
Greels
May 02, 2025 · 5 min read
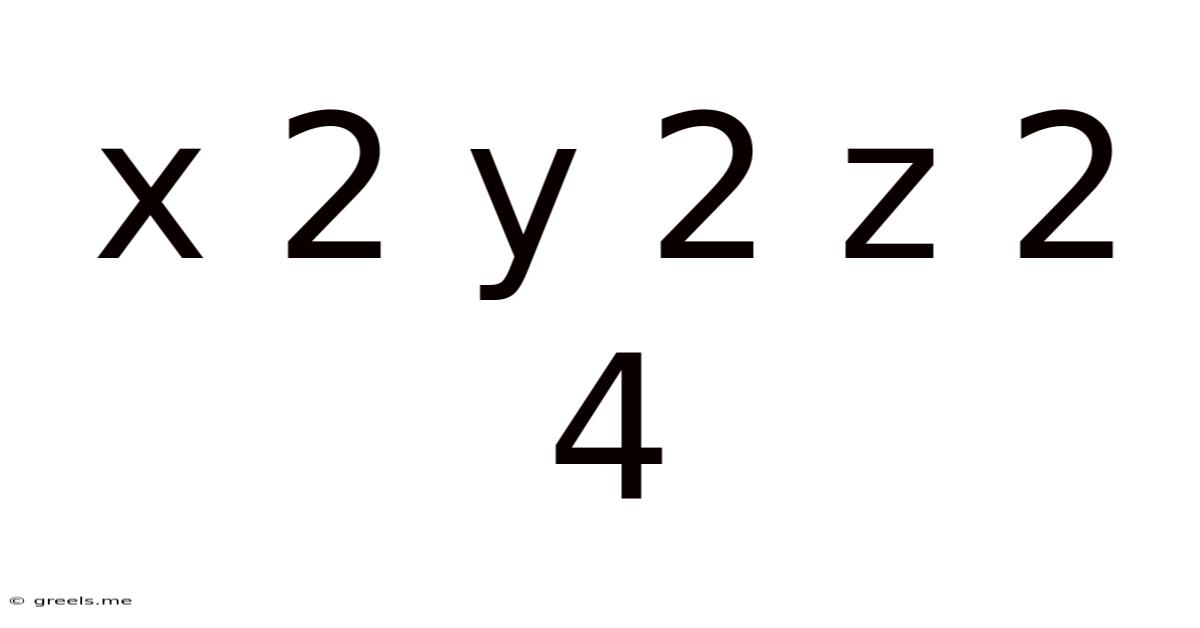
Table of Contents
Decoding the Equation: x² + y² + z² = 4 – A Deep Dive into Spheres, Geometry, and Number Theory
The seemingly simple equation, x² + y² + z² = 4, hides a wealth of mathematical richness. At first glance, it might appear to be just a basic algebraic expression. However, a closer examination reveals connections to three-dimensional geometry, number theory, and even abstract algebra. This article will explore this equation in depth, unveiling its geometric interpretation, its solutions within the realm of integers, and its implications in various mathematical fields.
The Geometric Interpretation: A Sphere in 3D Space
The most immediate interpretation of x² + y² + z² = 4 is its geometric representation. In three-dimensional Cartesian coordinates, this equation defines a sphere centered at the origin (0, 0, 0) with a radius of 2. This is because the equation represents the set of all points (x, y, z) that are exactly a distance of 2 from the origin. The distance formula in 3D space is derived directly from the Pythagorean theorem extended to three dimensions: √(x² + y² + z²). Setting this distance equal to 2 yields our equation.
Visualizing the Sphere: Understanding its Properties
Imagine a perfectly round ball floating in space. This ball perfectly embodies the equation x² + y² + z² = 4. Every point on the surface of the ball satisfies the equation, and no point inside or outside the ball does. This visualization is crucial to understanding the nature of the solutions. The sphere's properties – its radius, center, and surface area – are all directly related to the equation. The sphere's surface area, for example, can be calculated using the standard formula 4πr², where r is the radius (in this case, 2). Therefore, the surface area of this sphere is 16π.
Extending to Higher Dimensions: Hyperspheres
While we’re focusing on three dimensions, it's important to note that this type of equation can be extended to higher dimensions. In four dimensions, the equation x² + y² + z² + w² = 4 would represent a hypersphere. While we can't visualize these higher-dimensional shapes directly, their mathematical properties can be studied and understood using algebraic techniques.
Integer Solutions: A Number Theoretic Exploration
Beyond the geometric interpretation, the equation x² + y² + z² = 4 presents intriguing challenges in number theory. Finding integer solutions – meaning solutions where x, y, and z are all whole numbers – requires a different approach. This problem touches upon the topic of sums of squares, a well-studied area in number theory.
Finding Integer Solutions: Systematic Approaches
A brute-force approach to finding integer solutions might involve testing various combinations of integers. However, a more systematic approach is necessary to ensure that no solutions are missed. One method involves considering the possible values of x², y², and z². Since each of these is a perfect square, they must be non-negative integers. Given that the sum must equal 4, we can analyze the possible combinations.
Possible Combinations and Analysis:
- x² = 4, y² = 0, z² = 0: This yields the solutions (2, 0, 0), (-2, 0, 0), (0, 2, 0), (0, -2, 0), (0, 0, 2), (0, 0, -2).
- x² = 0, y² = 4, z² = 0: This yields similar solutions as above with different permutations.
- x² = 0, y² = 0, z² = 4: This also yields similar solutions.
- x² = 1, y² = 1, z² = 2: This combination is impossible since 2 is not a perfect square.
- Other combinations: Further analysis shows that no other combinations of perfect squares can add up to 4.
Therefore, there are a total of six integer solutions to the equation x² + y² + z² = 4. These are the only integer points that lie precisely on the surface of the sphere.
The Legendre's Three-Square Theorem and its Relevance
The problem of finding integer solutions to sums of squares is closely related to Legendre's three-square theorem. This theorem states that a natural number n can be represented as the sum of three squares of integers if and only if n is not of the form n = 4<sup>a</sup>(8b + 7) for non-negative integers a and b. In our case, 4 is clearly not of this form, so the theorem confirms the existence of integer solutions. However, it doesn't provide a direct method for finding all the solutions, which requires the combinatorial approach outlined above.
Extending the Equation: Variations and Applications
The equation x² + y² + z² = 4 serves as a foundation for exploring related mathematical concepts. By modifying or extending this equation, we can delve into a broader range of problems.
Variations on the Equation: Different Radii and Centers
Changing the constant on the right-hand side of the equation changes the radius of the sphere. For instance, x² + y² + z² = 9 represents a sphere with a radius of 3. Similarly, adding constants to x, y, or z shifts the center of the sphere away from the origin. This allows for the exploration of spheres with different locations and sizes.
Applications in Physics and Engineering: Spherical Coordinates
The equation x² + y² + z² = 4 finds applications in numerous fields, particularly those involving three-dimensional spatial relationships. In physics and engineering, spherical coordinates are often used to describe positions in space. The equation arises naturally when converting between Cartesian and spherical coordinates, simplifying calculations and simulations involving spheres.
Connections to Abstract Algebra and Group Theory: Groups of Rotations
The sphere represented by x² + y² + z² = 4 has inherent symmetries. The group of rotations that leave the sphere unchanged forms a significant mathematical structure. Exploring this group leads into more advanced areas of abstract algebra and group theory, demonstrating the depth and interconnectedness of mathematical concepts.
Conclusion: A Simple Equation with Profound Implications
The equation x² + y² + z² = 4, while seemingly simple, reveals a fascinating interplay between geometry, number theory, and abstract algebra. Its geometric interpretation as a sphere provides a visual understanding of its solutions, while its integer solutions delve into the rich world of sums of squares. Furthermore, its extensions and variations lead to more complex mathematical structures and applications in various scientific fields. This exploration highlights the beauty and interconnectedness of mathematics, demonstrating how a seemingly simple equation can unlock a wealth of knowledge and understanding. This journey through the equation is merely a starting point for deeper explorations into these complex and interconnected mathematical concepts. The continued study of this equation and its related ideas is a testament to the endless possibilities within the world of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.