Which Are The Solutions Of X2 13x 4
Greels
May 04, 2025 · 4 min read
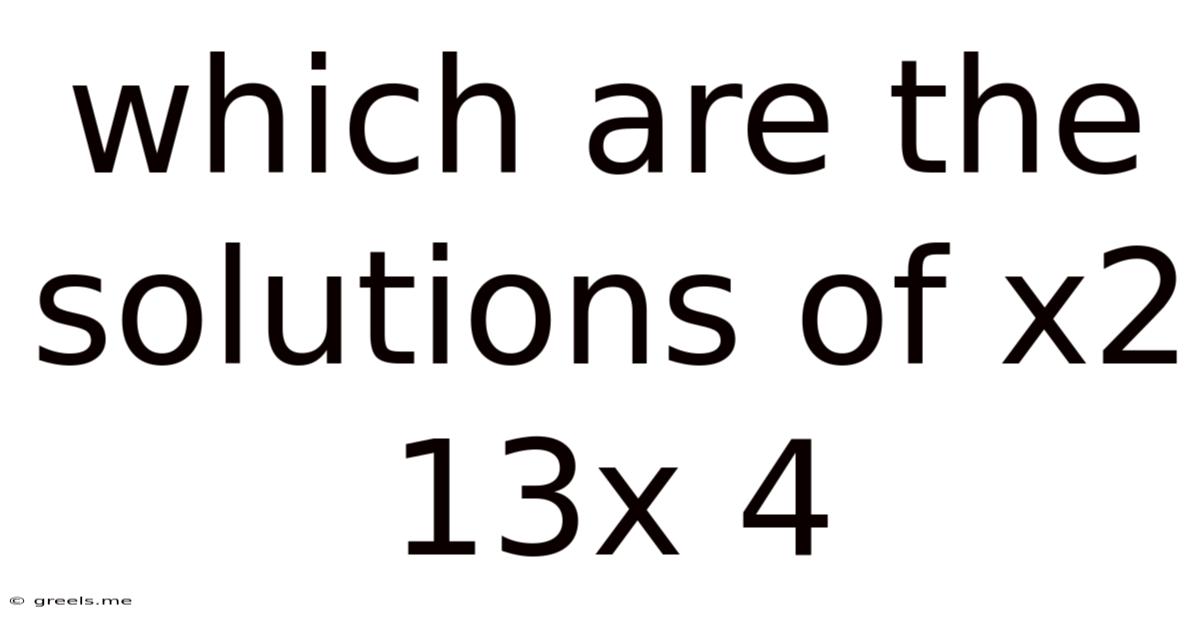
Table of Contents
Solving the Quadratic Equation: x² + 13x + 4 = 0
This article delves into the various methods for solving the quadratic equation x² + 13x + 4 = 0, providing a comprehensive understanding of the process and the implications of each approach. We'll explore both analytical and numerical techniques, examining their strengths and weaknesses in the context of this specific equation.
Understanding Quadratic Equations
Before we begin solving, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (x in this case) is 2. The general form is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our equation, x² + 13x + 4 = 0, we have a = 1, b = 13, and c = 4.
Method 1: Factoring
Factoring is a method of solving quadratic equations by expressing the quadratic as a product of two linear factors. This method is efficient when the factors are easily identifiable. However, it's not always applicable, especially when the roots are irrational or complex.
Let's attempt to factor x² + 13x + 4 = 0. We need to find two numbers that add up to 13 (the coefficient of x) and multiply to 4 (the constant term). Unfortunately, there are no two integers that satisfy these conditions. Therefore, factoring is not a viable method for this particular equation.
Method 2: Quadratic Formula
The quadratic formula is a universally applicable method for solving quadratic equations. It provides the roots directly, regardless of whether the equation is factorable or not. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 13, c = 4) into the quadratic formula, we get:
x = [-13 ± √(13² - 4 * 1 * 4)] / (2 * 1) x = [-13 ± √(169 - 16)] / 2 x = [-13 ± √153] / 2
Therefore, the two solutions are:
- x₁ = (-13 + √153) / 2 ≈ -0.311
- x₂ = (-13 - √153) / 2 ≈ -12.689
These are the exact solutions. The approximate values are provided for practical purposes.
Understanding the Discriminant
The expression inside the square root, b² - 4ac, is called the discriminant. It determines the nature of the roots:
- b² - 4ac > 0: Two distinct real roots (as in our case).
- b² - 4ac = 0: One real root (a repeated root).
- b² - 4ac < 0: Two complex conjugate roots.
In our equation, the discriminant (153) is positive, indicating two distinct real roots.
Method 3: Completing the Square
Completing the square is another algebraic method for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
To complete the square for x² + 13x + 4 = 0:
- Move the constant term to the right side: x² + 13x = -4
- Take half of the coefficient of x (13/2), square it ((13/2)² = 169/4), and add it to both sides: x² + 13x + 169/4 = -4 + 169/4
- Factor the left side as a perfect square: (x + 13/2)² = 153/4
- Take the square root of both sides: x + 13/2 = ±√(153/4)
- Solve for x: x = -13/2 ± √153/2
This yields the same solutions as the quadratic formula:
- x₁ = (-13 + √153) / 2
- x₂ = (-13 - √153) / 2
Method 4: Graphical Method
The graphical method involves plotting the quadratic function y = x² + 13x + 4 and finding the x-intercepts (where y = 0). These x-intercepts represent the solutions to the equation. While not as precise as algebraic methods for determining exact values, it provides a visual representation of the roots and their relationship to the parabola. Using graphing software or a calculator would be necessary for accurate plotting and determining the intercepts. The x-intercepts will correspond approximately to the values calculated using the quadratic formula.
Comparing the Methods
Each method has its advantages and disadvantages:
- Factoring: Simple and efficient when applicable, but not always possible.
- Quadratic Formula: Always works, provides exact solutions, but can be computationally more intensive.
- Completing the Square: Provides a good understanding of the underlying algebraic principles, but can be more complex than the quadratic formula for some equations.
- Graphical Method: Provides a visual representation, but less precise for determining exact solutions.
Applications of Quadratic Equations
Quadratic equations have numerous applications in various fields, including:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing stress and strain on materials.
- Economics: Modeling supply and demand, optimizing production.
- Computer Science: Developing algorithms, solving optimization problems.
Conclusion
Solving the quadratic equation x² + 13x + 4 = 0 demonstrates the versatility of different mathematical techniques. While factoring wasn't applicable in this specific case, the quadratic formula and completing the square provided the exact solutions: x₁ = (-13 + √153) / 2 and x₂ = (-13 - √153) / 2. The graphical method offers a visual approach, though less precise for finding the exact values. Understanding the different methods and their applicability is crucial for effectively solving a wide range of quadratic equations encountered in various fields. The choice of method often depends on the specific equation and the desired level of precision. The discriminant helps to predict the nature of the roots before embarking on the solution process, saving time and effort. This comprehensive analysis aims to provide a thorough understanding of the various approaches and their applications within the broader context of quadratic equations.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Are The Solutions Of X2 13x 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.