What Percent Of 50 Is 8
Greels
Apr 12, 2025 · 5 min read
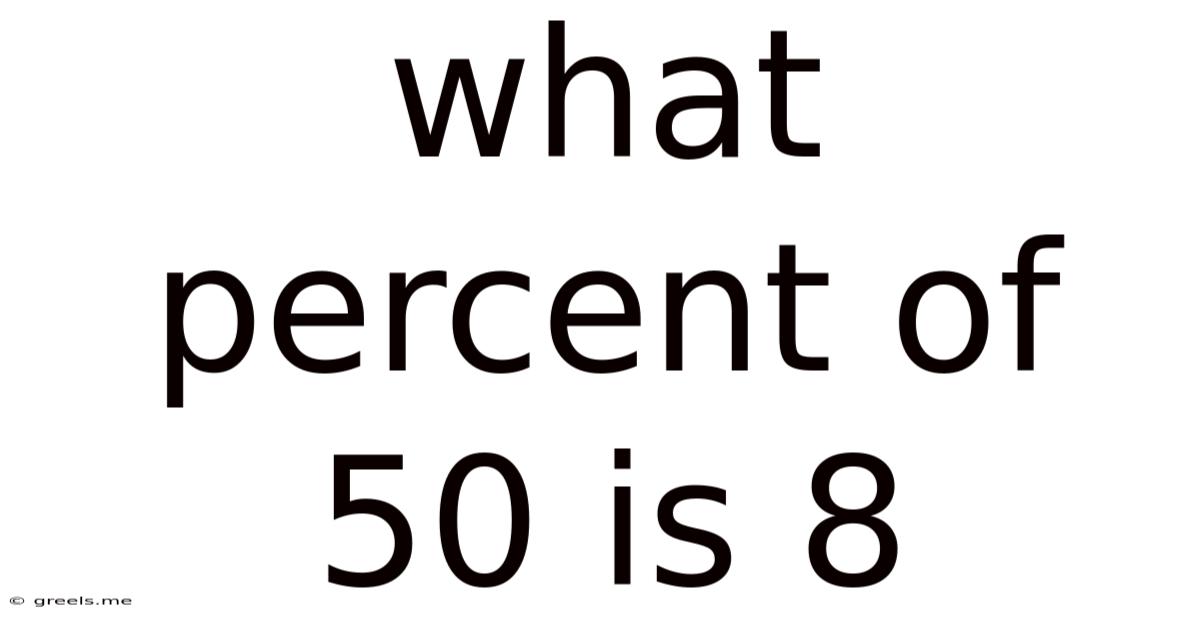
Table of Contents
What Percent of 50 is 8? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "What percent of 50 is 8?" – opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with wide-ranging applications in everyday life and various professional fields. This comprehensive guide will not only answer the question but also delve into the methods of calculating percentages, exploring different approaches and providing practical examples. We'll also touch upon the importance of understanding percentages in various real-world scenarios.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10.
Understanding this fundamental concept is crucial for tackling percentage calculations. Whether you're calculating discounts, interest rates, tax rates, or analyzing data, a firm grasp of percentages is essential.
Method 1: Using Proportions to Find the Percentage
This method relies on setting up a proportion to solve for the unknown percentage. We can represent the problem as follows:
- Part/Whole = Percentage/100
In our case:
- Part: 8
- Whole: 50
- Percentage: This is what we need to find (let's call it 'x')
So our proportion becomes:
- 8/50 = x/100
To solve for x, we can cross-multiply:
- 8 * 100 = 50 * x
- 800 = 50x
Now, divide both sides by 50:
- x = 800 / 50
- x = 16
Therefore, 8 is 16% of 50.
Method 2: Using the Percentage Formula
The percentage formula provides a more direct approach:
- Percentage = (Part / Whole) * 100
Substituting our values:
- Percentage = (8 / 50) * 100
- Percentage = 0.16 * 100
- Percentage = 16
Again, we arrive at the answer: 8 is 16% of 50.
Method 3: Decimal Conversion and Multiplication
This method involves converting the percentage to a decimal and then multiplying it by the whole number. While we're solving for the percentage here, we can illustrate the reverse process to show how this works. Let's say we want to find 16% of 50:
- Convert the percentage to a decimal: 16% = 16/100 = 0.16
- Multiply the decimal by the whole number: 0.16 * 50 = 8
This confirms our previous calculations: 16% of 50 is indeed 8.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently is invaluable in numerous real-world scenarios:
-
Retail Discounts: Calculating the final price of an item after a percentage discount is a common application. For example, a 20% discount on a $50 item means a saving of $10 (20% of $50), resulting in a final price of $40.
-
Taxes and Interest: Understanding percentage calculations is essential when dealing with taxes (sales tax, income tax) and interest rates (on loans, savings accounts). Calculating the total cost including tax, or the accumulated interest on a savings account, relies heavily on percentage calculations.
-
Financial Analysis: In finance, percentages are used extensively for analyzing financial statements, calculating returns on investments (ROI), and assessing risk. Understanding percentage changes in key financial metrics allows for informed decision-making.
-
Data Analysis and Statistics: Percentages are crucial for presenting and interpreting data. Expressing data as percentages makes comparisons easier and allows for a more intuitive understanding of trends and proportions within a dataset. For instance, understanding the percentage of a population that prefers a certain product provides valuable marketing insights.
-
Scientific Calculations: In various scientific fields, including chemistry, physics, and biology, percentages are utilized to express concentrations, efficiencies, and other quantitative relationships.
-
Everyday Life: Even in everyday scenarios, we use percentages. Whether it's tipping in a restaurant (calculating 15% or 20% of the bill), understanding sale prices in stores, or interpreting statistics in news reports, the ability to quickly calculate and interpret percentages is a valuable life skill.
Expanding on Percentage Problems: More Complex Scenarios
While the initial problem was straightforward, percentage calculations can become more complex. Consider these variations:
-
Finding the Whole when the Percentage and Part are Known: For example, if 20% of a number is 10, what is the number? This requires a slightly different approach, working backward from the percentage formula.
-
Finding the Percentage Increase or Decrease: Calculating the percentage change between two values requires understanding the concept of percentage change and applying the appropriate formula.
-
Compound Interest Calculations: Compound interest involves calculating interest on both the principal amount and accumulated interest over multiple periods, making the calculations more complex.
-
Dealing with Multiple Percentages: Situations may involve multiple percentage changes – for example, applying a discount and then a tax. Understanding the order of operations and how to correctly calculate the final amount is essential.
Mastering Percentages: Practice and Resources
Mastering percentage calculations requires practice. The more you work with different types of percentage problems, the more comfortable and proficient you will become. There are numerous online resources, including websites and educational apps, dedicated to helping you improve your skills in this area. Working through practice problems of varying difficulty will solidify your understanding and build confidence.
Conclusion: The Importance of Percentage Proficiency
The ability to perform percentage calculations accurately and efficiently is a fundamental skill applicable across a broad spectrum of activities. From everyday financial transactions to complex scientific analysis, understanding percentages is crucial for informed decision-making and problem-solving. This guide has provided a comprehensive overview of the various methods of calculating percentages, illustrated their practical applications, and highlighted the importance of mastering this crucial mathematical concept. By practicing and refining your skills, you'll be well-equipped to tackle percentage calculations confidently and effectively in any context.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 50 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.