What Percent Of 40 Is 70
Greels
Apr 03, 2025 · 4 min read
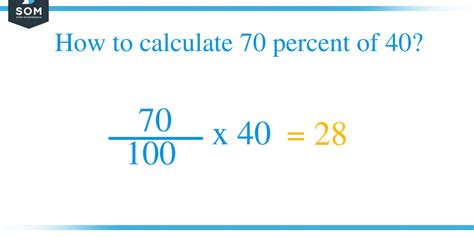
Table of Contents
What Percent of 40 is 70? Understanding Percentages and Proportions
This seemingly simple question, "What percent of 40 is 70?", opens the door to a deeper understanding of percentages, proportions, and their practical applications in everyday life. While the answer might seem counterintuitive at first glance (since 70 is larger than 40), the solution lies in mastering the fundamental concepts of percentage calculations. This article will not only provide the answer but also delve into the methodology, explore different approaches to solving similar problems, and discuss real-world examples where this type of calculation is crucial.
Understanding Percentages: A Quick Refresher
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" ("per" meaning "for each" and "cent" meaning "hundred"). For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this basic definition is critical for solving percentage problems.
Method 1: Using Proportions to Solve "What percent of 40 is 70?"
The most straightforward way to approach this problem is to set up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the following proportion:
- x/100 = 70/40
Where:
- x represents the percentage we're trying to find.
- 70 is the part (the number we're comparing to the whole).
- 40 is the whole (the base number).
- 100 represents the total percentage.
To solve for x, we can cross-multiply:
- 40x = 7000
Then, divide both sides by 40:
- x = 175
Therefore, 70 is 175% of 40.
Method 2: Using the Percentage Formula
The percentage formula provides another effective way to solve this problem. The formula is:
- Percentage = (Part / Whole) * 100
In our case:
- Part = 70
- Whole = 40
Substituting these values into the formula:
- Percentage = (70 / 40) * 100
- Percentage = 1.75 * 100
- Percentage = 175%
This confirms our previous result.
Why is the Percentage Greater Than 100%?
It's important to understand that percentages can be greater than 100%. This simply means that the "part" is larger than the "whole." In our example, 70 is more than 40, hence the resulting percentage (175%) is greater than 100%. This scenario frequently arises in contexts like growth percentages, increase in value, or comparing quantities where one exceeds the other.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life, including:
- Finance: Calculating interest rates, discounts, tax percentages, profit margins, and investment returns.
- Retail: Determining sale prices, discounts, and markups.
- Statistics: Representing data as percentages in charts, graphs, and reports. Analyzing survey results and interpreting statistical significance.
- Science: Expressing concentrations of solutions, measuring changes in variables over time, and interpreting experimental data.
- Education: Calculating grades, scores, and overall performance.
- Health: Representing disease prevalence, treatment success rates, and risk factors.
Solving Similar Percentage Problems: A Step-by-Step Guide
Let's explore how to solve similar problems using the methods described above.
Problem 1: What percent of 60 is 30?
Method 1 (Proportions):
- x/100 = 30/60
- 60x = 3000
- x = 50
Method 2 (Percentage Formula):
- Percentage = (30 / 60) * 100 = 50%
Answer: 30 is 50% of 60.
Problem 2: What percent of 25 is 15?
Method 1 (Proportions):
- x/100 = 15/25
- 25x = 1500
- x = 60
Method 2 (Percentage Formula):
- Percentage = (15 / 25) * 100 = 60%
Answer: 15 is 60% of 25.
Problem 3: What percent of 120 is 180?
Method 1 (Proportions):
- x/100 = 180/120
- 120x = 18000
- x = 150
Method 2 (Percentage Formula):
- Percentage = (180 / 120) * 100 = 150%
Answer: 180 is 150% of 120.
Beyond the Basics: Advanced Percentage Concepts
While the examples above focus on basic percentage calculations, there are more advanced concepts to explore:
- Compound interest: Interest calculated on both the principal amount and accumulated interest.
- Percentage change: Calculating the percentage increase or decrease between two values.
- Percentage points: The difference between two percentages, not to be confused with percentage change.
- Weighted averages: Calculating averages where different values have different weights or importance.
Mastering percentage calculations is a valuable skill with broad applications across numerous fields. By understanding the fundamental principles, employing different solution methods, and practicing regularly, you'll become proficient in solving percentage problems and confidently tackling real-world scenarios involving proportions and percentages. Remember to always clearly identify the "part" and the "whole" before starting the calculation to avoid errors. This will ensure accuracy and confidence in your percentage calculations.
Latest Posts
Latest Posts
-
How Many Cm Is 61 Inches
Apr 04, 2025
-
96 Cm Is How Many Inches
Apr 04, 2025
-
How Many Cm In 38 Inches
Apr 04, 2025
-
How Long Is 800 Seconds In Minutes
Apr 04, 2025
-
How Many Oz Is 230 Grams
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 40 Is 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
