What Is Ten Percent Of 200
Greels
Apr 02, 2025 · 5 min read
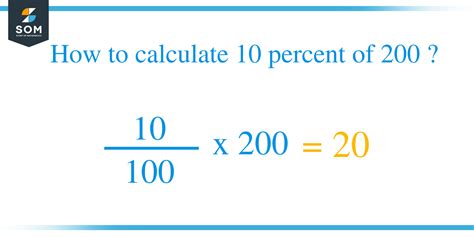
Table of Contents
What is Ten Percent of 200? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is ten percent of 200?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (20), understanding the underlying principles and exploring the various contexts in which percentage calculations are used provides valuable insight into a fundamental aspect of mathematics and its relevance to everyday life. This article will not only answer the initial question but delve into the broader topic of percentages, offering various methods for calculation, exploring real-world examples, and highlighting the importance of percentage understanding in various fields.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" or "out of 100." The symbol used to represent percentages is the percent sign, %. Therefore, 10% can be interpreted as 10 out of 100, or 10/100, which simplifies to the decimal 0.1.
This fundamental understanding is crucial for tackling any percentage calculation. The formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
Applying this to our initial question:
(10/100) * 200 = 20
Therefore, ten percent of 200 is 20.
Different Methods for Calculating Percentages
While the above formula is the most common and straightforward, there are other methods to calculate percentages, each offering its own advantages depending on the context and the individual's mathematical preference:
-
Using Decimal Equivalents: As mentioned earlier, a percentage can be expressed as a decimal. 10% is equivalent to 0.1. Therefore, you can simply multiply the number (200) by the decimal equivalent (0.1): 0.1 * 200 = 20. This method is often faster for mental calculations.
-
Using Fractions: Percentages can also be represented as fractions. 10% is equivalent to 10/100, which simplifies to 1/10. Therefore, you can calculate 1/10 of 200: (1/10) * 200 = 20. This method is particularly useful when dealing with simpler percentages.
-
Using Proportions: Percentages can be solved using proportions. You can set up a proportion: 10/100 = x/200, where 'x' represents the unknown value. Cross-multiplying and solving for 'x' will give you the answer: 10 * 200 = 100 * x, therefore x = 20. This method is helpful for understanding the underlying relationship between the percentage and the whole.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life, extending far beyond simple mathematical exercises. Here are just a few examples:
-
Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. For example, a 20% discount on a $100 item means you save $20 (20% of $100). Understanding percentages is vital for savvy shoppers to compare prices and maximize savings.
-
Taxes: Sales tax, income tax, and other taxes are often calculated as a percentage of the taxable amount. Knowing how to calculate percentages helps individuals understand their tax obligations accurately.
-
Tips and Gratuities: When dining out, it's customary to leave a tip, usually expressed as a percentage of the bill. A 15% tip on a $50 meal would be $7.50 (15% of $50).
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Financial Statements: Percentage changes in financial data are commonly used to track performance. For example, comparing the percentage increase or decrease in revenue or profit year-over-year provides crucial insights into a business's financial health.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. They allow for easy comparison of proportions across different datasets. For example, understanding the percentage of a population that supports a particular political candidate provides valuable insight into public opinion.
-
Scientific Applications: Percentages are also used extensively in scientific fields. For instance, expressing the concentration of a solution as a percentage indicates the amount of solute relative to the total solution. In ecology, percentages can show the proportion of various species within an ecosystem.
Beyond the Basics: More Complex Percentage Problems
While calculating 10% of 200 is relatively simple, more complex percentage problems frequently arise in various contexts. These often involve calculating:
-
Percentage Increase or Decrease: Determining the percentage change between two values requires understanding both the initial and final values. For example, finding the percentage increase from 100 to 120 would involve calculating the difference (20) divided by the initial value (100), then multiplying by 100% to express it as a percentage.
-
Finding the Original Value: If you know the final value after a percentage increase or decrease, and the percentage change, you can calculate the original value using algebraic equations.
-
Compound Interest: This involves calculating interest not just on the principal amount but also on accumulated interest. Understanding compound interest is crucial for making informed decisions about investments and loans.
Mastering Percentages: Practice and Resources
Becoming proficient in percentage calculations requires consistent practice. Start with simple problems like "What is ten percent of 200?" and gradually work your way up to more complex scenarios. Numerous online resources, including educational websites, calculators, and interactive exercises, can help you enhance your understanding and skills.
Conclusion: The Significance of Percentage Understanding
The seemingly simple calculation of "What is ten percent of 200?" unveils a fundamental mathematical concept with far-reaching implications in various aspects of life. From personal finance and shopping to scientific research and data analysis, the ability to calculate and interpret percentages is a valuable skill that enhances decision-making and problem-solving capabilities. By understanding the various methods for calculating percentages and exploring their applications in diverse contexts, individuals can better navigate the complexities of the modern world and unlock opportunities for growth and success. Mastering percentages isn't merely about solving mathematical equations; it's about developing a crucial life skill with practical value across numerous fields.
Latest Posts
Latest Posts
-
What Day Is It In 9 Days
Apr 03, 2025
-
How Many Meters Is 500 Feet
Apr 03, 2025
-
How Tall Is 1 62m In Feet
Apr 03, 2025
-
3000 Meters Is How Many Feet
Apr 03, 2025
-
How Many Pounds In 55 Kilograms
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is Ten Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
