What Is 60 Percent Of 25
Greels
May 22, 2025 · 4 min read
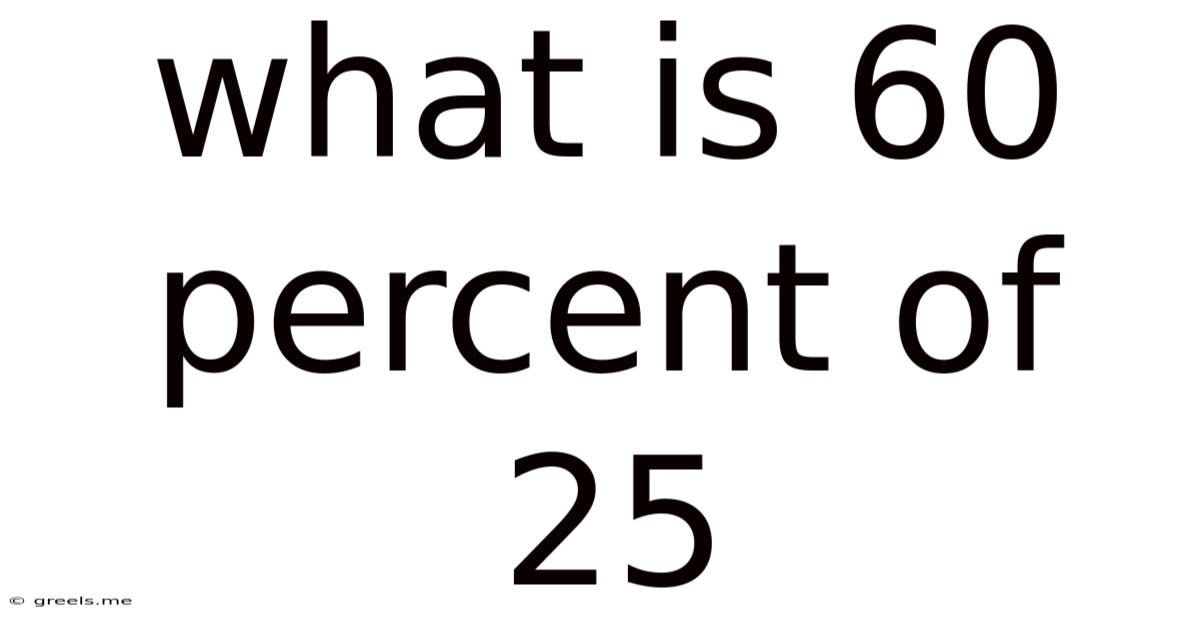
Table of Contents
What is 60 Percent of 25? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 60 percent of 25?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (15), understanding the process and the broader implications of percentages is crucial for numerous aspects of life, from personal finance to advanced statistical analysis. This article will delve into the calculation, explore various methods to solve percentage problems, and demonstrate the widespread utility of percentages across diverse fields.
Calculating 60% of 25: The Fundamentals
The most fundamental approach involves translating the problem into a mathematical equation. "60 percent of 25" can be written as:
0.60 x 25 = 15
Here's a breakdown:
- 60 percent: We convert the percentage to a decimal by dividing by 100 (60/100 = 0.60). This represents the fraction 60/100, or 3/5.
- of: In mathematical terms, "of" signifies multiplication.
- 25: This is the whole number or base value we're finding the percentage of.
Therefore, multiplying 0.60 by 25 directly yields the answer: 15.
Alternative Methods for Calculating Percentages
While the decimal method is efficient, other methods offer alternative approaches and enhance understanding:
1. Fraction Method:
As mentioned earlier, 60% is equivalent to the fraction 3/5. Therefore, the problem becomes:
(3/5) x 25 = 15
This method involves simplifying the fraction before multiplication. Here, 25 divided by 5 equals 5, leaving 3 x 5 = 15. This method is particularly useful when dealing with simpler fractions.
2. Proportion Method:
This method uses the concept of ratios and proportions. We can set up a proportion:
60/100 = x/25
Where 'x' represents the unknown value (60% of 25). Cross-multiplying gives:
60 x 25 = 100x
1500 = 100x
Dividing both sides by 100 gives:
x = 15
3. Using a Calculator:
Modern calculators greatly simplify percentage calculations. Most calculators have a percentage key (%) that directly performs the calculation. Simply input "60 % x 25 =" to obtain the result: 15.
The Importance of Understanding Percentages
The ability to calculate percentages extends far beyond simple mathematical exercises. Percentages are essential tools in various aspects of life:
1. Personal Finance:
- Interest Rates: Understanding interest rates on loans, savings accounts, and investments relies heavily on percentage calculations. Calculating interest earned or paid involves directly applying percentage calculations.
- Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. Calculating the final price after a discount requires understanding percentage reductions.
- Taxes: Sales taxes, income taxes, and other taxes are often expressed as percentages of the taxable amount. Calculating tax amounts requires accurately determining percentages.
- Tips and Gratuities: Calculating appropriate tips in restaurants or other service settings involves determining a percentage of the total bill.
- Budgeting: Allocating a certain percentage of income to different categories (savings, housing, food, etc.) is crucial for effective financial planning.
2. Business and Economics:
- Profit Margins: Businesses use percentage calculations to determine profit margins – the percentage of revenue that represents profit.
- Market Share: Analyzing market share often involves calculating the percentage of a market held by a specific company or product.
- Growth Rates: Tracking economic growth, sales growth, or population growth frequently involves expressing these changes as percentages.
- Inflation Rates: Inflation is typically measured as a percentage increase in the price level of goods and services over a period.
- Investment Returns: Evaluating investment performance necessitates calculating percentage returns on investments.
3. Science and Statistics:
- Data Analysis: Many statistical analyses involve calculating percentages to represent proportions or frequencies within datasets.
- Experimental Results: Scientists often express experimental results as percentages to show the magnitude of effects or changes.
- Probability and Risk Assessment: Probabilities are often expressed as percentages to indicate the likelihood of events occurring.
- Survey Results: Representing the results of surveys or polls frequently involves presenting data as percentages.
4. Everyday Life:
- Recipes: Scaling recipes up or down involves adjusting ingredient quantities based on percentages.
- Measurements: Expressing proportions or quantities in percentages can simplify certain measurements and calculations.
- Discounts and Sales: As mentioned earlier, everyday shopping often involves calculating percentage discounts.
Advanced Applications of Percentage Calculations
Beyond the basic calculations, more advanced applications of percentages exist:
- Compound Interest: Calculating compound interest, which involves earning interest on both principal and accumulated interest, requires iterative percentage calculations.
- Percentage Change: Determining the percentage increase or decrease between two values provides a comparative measure of change.
- Percentage Points: Differentiating between percentage points and percentage change is crucial for accurate interpretation. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Conclusion
The question "What is 60 percent of 25?" serves as a gateway to a deeper understanding of percentages and their multifaceted applications. While the answer is simply 15, the underlying principles and their practical implications are far-reaching. Mastering percentage calculations is crucial for navigating various aspects of personal finance, business, science, and everyday life. By understanding the different methods of calculation and recognizing the diverse contexts where percentages are applied, individuals can enhance their numerical literacy and make informed decisions in various domains. The seemingly simple calculation holds the key to a world of practical and analytical power.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.