What Is 60 Percent Of 20
Greels
Apr 01, 2025 · 5 min read
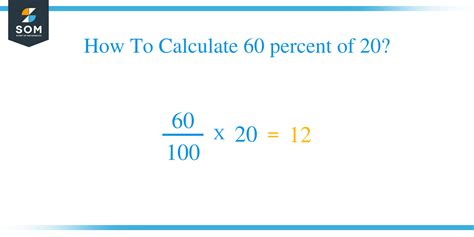
Table of Contents
What is 60 Percent of 20? A Deep Dive into Percentages and Their Applications
Finding 60 percent of 20 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying principles of percentages and their diverse applications extends far beyond this basic calculation. This article will not only answer the question "What is 60 percent of 20?" but also delve into the broader context of percentages, their practical uses, and how to calculate them efficiently.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 60 percent means 60 out of 100, or 60/100. This can be simplified to 3/5. Understanding this fundamental concept is crucial for tackling any percentage calculation.
Key Components of Percentage Calculations
Three key components are involved in percentage problems:
- The Percentage: This is the rate or proportion, often represented by the symbol "%". In our example, the percentage is 60%.
- The Whole: This is the total amount or the base value upon which the percentage is calculated. In our case, the whole is 20.
- The Part: This is the result of the percentage calculation – the portion of the whole represented by the given percentage. This is what we need to find.
Calculating 60 Percent of 20
There are several ways to calculate 60 percent of 20. Let's explore the most common methods:
Method 1: Using the Fraction Method
Since 60% is equivalent to 60/100 or 3/5, we can express the problem as:
(3/5) * 20 = 12
Therefore, 60 percent of 20 is 12.
Method 2: Using Decimal Conversion
Converting the percentage to a decimal simplifies the calculation. To do this, divide the percentage by 100:
60% ÷ 100 = 0.60
Now, multiply the decimal by the whole:
0.60 * 20 = 12
Again, we arrive at the answer: 60 percent of 20 is 12.
Method 3: Using Proportion
We can set up a proportion to solve this problem:
60/100 = x/20
Cross-multiplying, we get:
100x = 60 * 20
100x = 1200
x = 1200/100
x = 12
Thus, 60 percent of 20 is 12.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in various real-world scenarios:
1. Financial Calculations:
- Interest Rates: Calculating simple and compound interest relies heavily on percentage calculations. Understanding interest rates is crucial for managing loans, investments, and savings accounts.
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Being able to quickly determine the discounted price is a valuable consumer skill. For instance, a 20% discount on a $50 item is calculated as 0.20 * $50 = $10 discount, resulting in a final price of $40.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the total amount. Calculating the tax amount and the total cost including taxes requires percentage calculations.
- Profit Margins: Businesses use percentages to determine profit margins—the difference between the cost of goods and the selling price, expressed as a percentage of the selling price.
2. Statistical Analysis:
- Data Representation: Percentages are used extensively in presenting statistical data, making it easier to understand and compare different values. For example, expressing survey results as percentages allows for easy comparison across different demographics.
- Probability and Odds: Percentages are used to represent probabilities and odds in various contexts, such as weather forecasting, game theory, and risk assessment.
3. Everyday Life:
- Tip Calculation: Calculating tips in restaurants is a common application of percentages. A 15% tip on a $30 meal is 0.15 * $30 = $4.50.
- Grade Calculation: Grades in many educational systems are often expressed as percentages.
- Recipe Scaling: Adjusting recipe quantities based on the number of servings often involves percentage calculations. If a recipe calls for 2 cups of flour and you want to make half the recipe, you would use 50% of 2 cups, which is 1 cup.
Advanced Percentage Calculations
While calculating 60 percent of 20 is straightforward, more complex percentage problems might require additional steps. Here are some examples:
1. Finding the Percentage Increase or Decrease
Suppose a quantity increases from 20 to 25. To calculate the percentage increase, follow these steps:
- Find the difference: 25 - 20 = 5
- Divide the difference by the original amount: 5 / 20 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
Therefore, the quantity increased by 25%.
Similarly, if a quantity decreases from 20 to 15, the percentage decrease is calculated as:
- Difference: 20 - 15 = 5
- Divide by the original amount: 5 / 20 = 0.25
- Multiply by 100: 0.25 * 100 = 25%
The quantity decreased by 25%.
2. Finding the Original Amount
Let's say 60% of an unknown amount is 12. To find the original amount, we set up an equation:
0.60 * x = 12
Solving for x:
x = 12 / 0.60
x = 20
The original amount is 20.
3. Calculating Percentage Change with Different Base Values
Imagine a situation where the base value changes over time. Calculating the percentage change across multiple periods requires careful attention to the base value used in each calculation.
For example, if a value increases from 10 to 15 and then from 15 to 20, the percentage increase in each period is different. The first period shows a 50% increase (5/10 * 100), while the second period shows a 33.33% increase (5/15 * 100). It's crucial to clarify which base value is being used to avoid confusion and ensure accurate interpretations.
Conclusion: Mastering Percentages for a Data-Driven World
The simple question "What is 60 percent of 20?" opens the door to a vast world of percentage calculations and their applications across various fields. From basic arithmetic to complex financial modeling and statistical analysis, the ability to confidently handle percentages is a vital skill in today's data-driven world. By understanding the fundamental principles, mastering different calculation methods, and practicing with real-world scenarios, you can confidently navigate the world of percentages and harness their power for informed decision-making. Remember to always double-check your calculations and choose the method that feels most intuitive and efficient for you. The answer remains consistent—60 percent of 20 is indeed 12. But the understanding gained by exploring the underlying concepts is far more valuable.
Latest Posts
Latest Posts
-
Solve For Simplify Your Answer As Much As Possible
Apr 02, 2025
-
109 Inches Is How Many Feet
Apr 02, 2025
-
3 X 1 2 X 1
Apr 02, 2025
-
How Many Pounds Is 350 G
Apr 02, 2025
-
90 Is What Percent Of 60
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
