What Is 50 Percent Of 25
Greels
May 20, 2025 · 4 min read
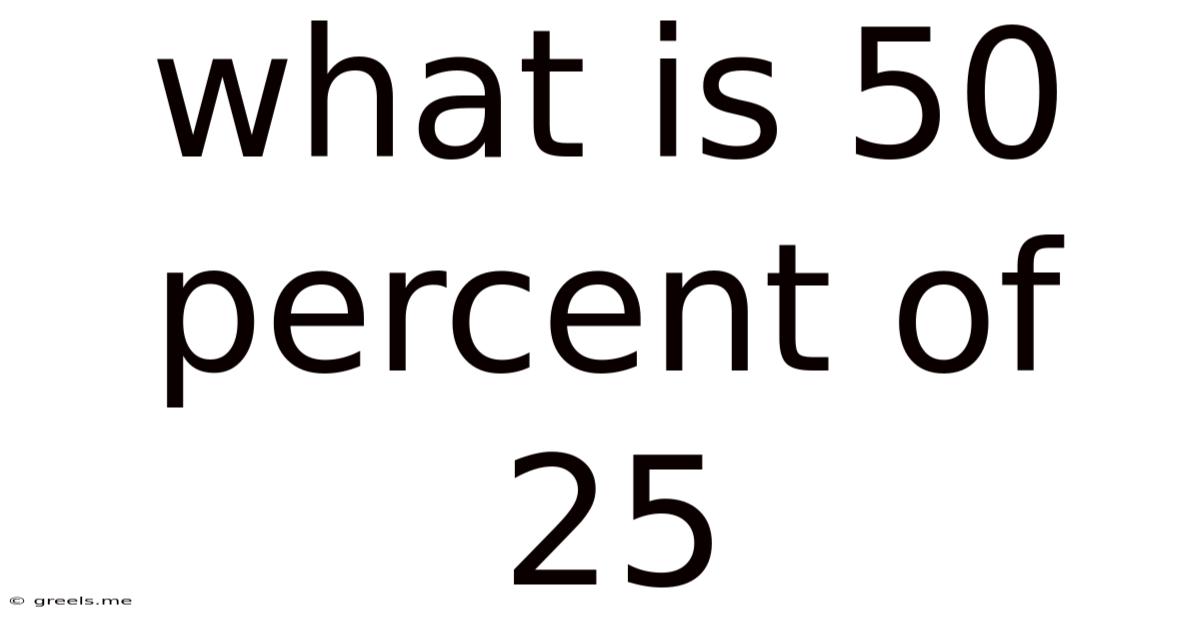
Table of Contents
What is 50 Percent of 25? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 50 percent of 25?", opens the door to a broader understanding of percentages, their practical applications, and how they're used in everyday life and complex calculations. While the answer itself is straightforward, exploring the methodology behind it reveals fundamental mathematical concepts with far-reaching implications.
Understanding Percentages: The Basics
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% is equivalent to 50/100, which simplifies to 1/2 or 0.5 in decimal form. This representation is crucial for performing percentage calculations.
Key Concepts in Percentage Calculations:
- The Whole: This is the total amount or value you're considering. In our question, the whole is 25.
- The Percentage: This is the fraction (expressed as a percentage) of the whole that we're interested in finding. In our case, it's 50%.
- The Part: This is the result of the calculation – the portion of the whole representing the given percentage. This is what we need to determine.
Calculating 50 Percent of 25: The Methods
There are several ways to calculate 50% of 25. Let's explore the most common approaches:
Method 1: Using the Fraction Equivalent
Since 50% is equivalent to 1/2, calculating 50% of 25 is the same as finding half of 25. This is a simple division problem:
25 ÷ 2 = 12.5
Therefore, 50% of 25 is 12.5.
Method 2: Converting to Decimal
We can also convert 50% to its decimal equivalent (0.5) and then multiply it by the whole number (25):
0.5 × 25 = 12.5
This method yields the same result: 12.5.
Method 3: Using a Proportion
Setting up a proportion can be helpful for understanding the relationship between the percentage, the whole, and the part. We can express the problem as follows:
50/100 = x/25
Here, 'x' represents the unknown part we're trying to find. To solve for 'x,' we cross-multiply:
50 × 25 = 100 × x
1250 = 100x
x = 1250 ÷ 100
x = 12.5
Again, the answer remains 12.5.
Expanding the Concept: Beyond 50% of 25
Understanding how to calculate 50% of 25 provides a foundation for tackling more complex percentage problems. Let's explore some related scenarios:
Finding Other Percentages of 25:
Using the same methods described above, we can easily calculate other percentages of 25. For example:
- 25% of 25: (0.25 x 25) = 6.25
- 75% of 25: (0.75 x 25) = 18.75
- 10% of 25: (0.10 x 25) = 2.5
- 1% of 25: (0.01 x 25) = 0.25
Calculating Percentages of Different Numbers:
The principles remain the same when calculating percentages of different numbers. For instance, to find 50% of 100:
- Using the fraction method: 100 ÷ 2 = 50
- Using the decimal method: 0.5 x 100 = 50
Finding the Percentage One Number Represents of Another:
This involves a slightly different calculation. Let's say we want to know what percentage 10 represents of 25. We set up the following equation:
x/100 = 10/25
Cross-multiplying and solving for x gives us:
25x = 1000
x = 40
Therefore, 10 represents 40% of 25.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and professional fields. Here are some examples:
Finance and Budgeting:
- Calculating discounts: Sales often advertise discounts as percentages (e.g., 20% off). Understanding percentages is essential for determining the actual price after a discount is applied.
- Understanding interest rates: Interest rates on loans, savings accounts, and investments are expressed as percentages.
- Analyzing financial statements: Financial reports use percentages extensively to represent ratios, growth rates, and profitability.
- Tax calculations: Taxes are often calculated as a percentage of income or the value of goods and services.
Science and Statistics:
- Representing data: Percentages are frequently used to present data in a clear and concise way, such as in charts and graphs.
- Calculating probabilities: Probability is often expressed as a percentage.
- Statistical analysis: Many statistical measures, such as percentages, proportions, and rates, rely heavily on percentage calculations.
Everyday Life:
- Calculating tips: Restaurant tips are often calculated as a percentage of the total bill.
- Understanding nutritional information: Nutritional labels express the percentage of daily recommended values for various nutrients.
- Estimating quantities: Percentages help in making quick estimations, like figuring out the amount of ingredients needed for a recipe based on a scaled-down or scaled-up version.
Conclusion: The Significance of Percentage Calculations
While the initial question, "What is 50 percent of 25?", may seem simplistic, it serves as a springboard to explore the fundamental concepts of percentages and their broad applications. Mastering percentage calculations is not merely a mathematical skill; it's a crucial tool for navigating various aspects of our daily lives, from personal finances to professional endeavors. The ability to quickly and accurately calculate percentages empowers informed decision-making and a deeper understanding of numerical data presented in various contexts. The various methods presented here – using fractions, decimals, or proportions – provide flexibility and adaptability when dealing with a range of percentage-related problems. As you continue to practice and apply these techniques, your comfort and proficiency in handling percentage calculations will naturally increase.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 50 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.