What Is 5 Percent Of 2500
Greels
Apr 05, 2025 · 5 min read
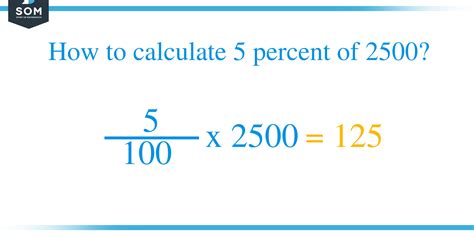
Table of Contents
What is 5 Percent of 2500? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous areas of life, from everyday finances to complex scientific calculations. Understanding how to determine a percentage of a number is crucial for budgeting, comparing prices, understanding discounts, and much more. This article will comprehensively explore how to calculate 5% of 2500, explaining the process step-by-step and then expanding on the broader implications of percentage calculations.
Understanding Percentages
Before diving into the calculation, let's establish a solid understanding of what percentages represent. A percentage is simply a fraction expressed as a portion of 100. The symbol "%" signifies "per hundred" or "out of 100". For instance, 5% can be written as 5/100 or 0.05 as a decimal. This means that 5% represents 5 parts out of every 100 parts.
Calculating 5% of 2500: The Step-by-Step Guide
There are several ways to calculate 5% of 2500. Here are three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. As mentioned earlier, 5% is equivalent to 0.05. Therefore, to find 5% of 2500, we simply multiply 2500 by 0.05:
2500 x 0.05 = 125
Therefore, 5% of 2500 is 125.
Method 2: Using the Fraction Equivalent
We can also express 5% as the fraction 5/100. To calculate 5% of 2500, we multiply 2500 by 5/100:
2500 x (5/100) = (2500 x 5) / 100 = 12500 / 100 = 125
Again, we arrive at the answer: 5% of 2500 is 125.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and the whole. We can set up a proportion:
5/100 = x/2500
Where 'x' represents the unknown value (5% of 2500). To solve for x, we cross-multiply:
100x = 5 x 2500
100x = 12500
x = 12500 / 100
x = 125
This confirms once more that 5% of 2500 is 125.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly versatile and has widespread applications in various fields:
Finance and Budgeting:
- Calculating Sales Tax: Understanding sales tax percentages is crucial for budgeting and comparing prices. If sales tax is 6%, you can easily calculate the total cost of an item by calculating 6% of its price and adding it to the original cost.
- Determining Discounts: Discount percentages are frequently used in retail. If an item is discounted by 20%, you can calculate the final price by subtracting 20% of the original price from the original price.
- Calculating Interest: Interest rates on loans and savings accounts are expressed as percentages. Understanding how to calculate interest is essential for managing personal finances.
- Investment Returns: Investment returns are also typically expressed as percentages. Tracking the percentage growth or decline of your investments allows for effective financial planning.
- Analyzing Financial Statements: Financial statements often utilize percentages to show ratios and trends, such as profit margins and debt-to-equity ratios.
Science and Statistics:
- Data Analysis: Percentages are extensively used in presenting and interpreting data in scientific studies and statistical analyses. For example, representing survey results or experimental outcomes often involves calculating percentages.
- Probability and Statistics: Probability is often expressed as a percentage, indicating the likelihood of an event occurring.
- Scientific Measurements: In various scientific fields, percentage error or percentage change are frequently used to quantify the accuracy and precision of measurements.
Everyday Life:
- Tipping in Restaurants: Calculating tips is a common application of percentages. A 15% or 20% tip on a restaurant bill requires calculating a percentage of the total bill amount.
- Understanding Nutritional Information: Food labels often express nutrient content as percentages of recommended daily values.
- Comparing Prices: Percentages can help in comparing prices of different products or services, particularly when dealing with sales or discounts.
- Understanding Survey Results: News reports and articles frequently present survey results using percentages to summarize public opinion or consumer behavior.
Beyond the Basics: Advanced Percentage Calculations
While calculating 5% of 2500 is relatively simple, many real-world scenarios require more complex percentage calculations. Here are a few examples:
- Calculating Percentage Increase or Decrease: This involves finding the percentage change between two values. For example, if a value increases from 100 to 120, the percentage increase is calculated as: [(120 - 100) / 100] x 100% = 20%.
- Finding the Original Value After a Percentage Change: If a value has increased by a certain percentage and you know the final value, you can work backward to find the original value. For instance, if a value is increased by 10% to reach 220, the original value was 200.
- Compounding Percentages: This is crucial in situations involving compound interest, where interest earned in one period is added to the principal, and the next period's interest is calculated on the new, larger amount.
- Working with Multiple Percentages: In many situations, you need to deal with multiple percentage changes in sequence. For example, calculating the final price after a series of discounts or markups.
Mastering Percentages: Tools and Resources
While manual calculation is valuable for understanding the underlying concepts, several tools can help with faster and more complex percentage calculations:
- Calculators: Most calculators have a percentage function, simplifying calculations significantly.
- Spreadsheet Software (e.g., Excel, Google Sheets): These programs provide built-in functions for percentage calculations, making it easy to work with large datasets or complex scenarios.
- Online Percentage Calculators: Numerous websites offer free online percentage calculators, providing a convenient way to perform various percentage calculations.
Conclusion: The Importance of Percentage Literacy
The ability to calculate percentages is a fundamental skill with far-reaching implications across various aspects of life. Mastering percentage calculations, from the simplest to the most complex, empowers individuals to make informed decisions, analyze data effectively, and navigate the numerical world with confidence. Understanding the methods outlined in this article, coupled with the use of available tools, ensures proficiency in this essential mathematical skill, improving decision-making capabilities in both personal and professional contexts. From budgeting to investment strategies, understanding percentages is key to financial literacy and overall success.
Latest Posts
Latest Posts
-
70 Millas Por Hora A Km H
Apr 06, 2025
-
18 Centimeters Equals How Many Inches
Apr 06, 2025
-
How Many Pounds Is 4 6 Kg
Apr 06, 2025
-
Cuanto Son 132 Libras En Kilos
Apr 06, 2025
-
How Much Is 1 25 Kg In Pounds
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 2500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
