What Is 5 Percent Of 25
Greels
May 21, 2025 · 5 min read
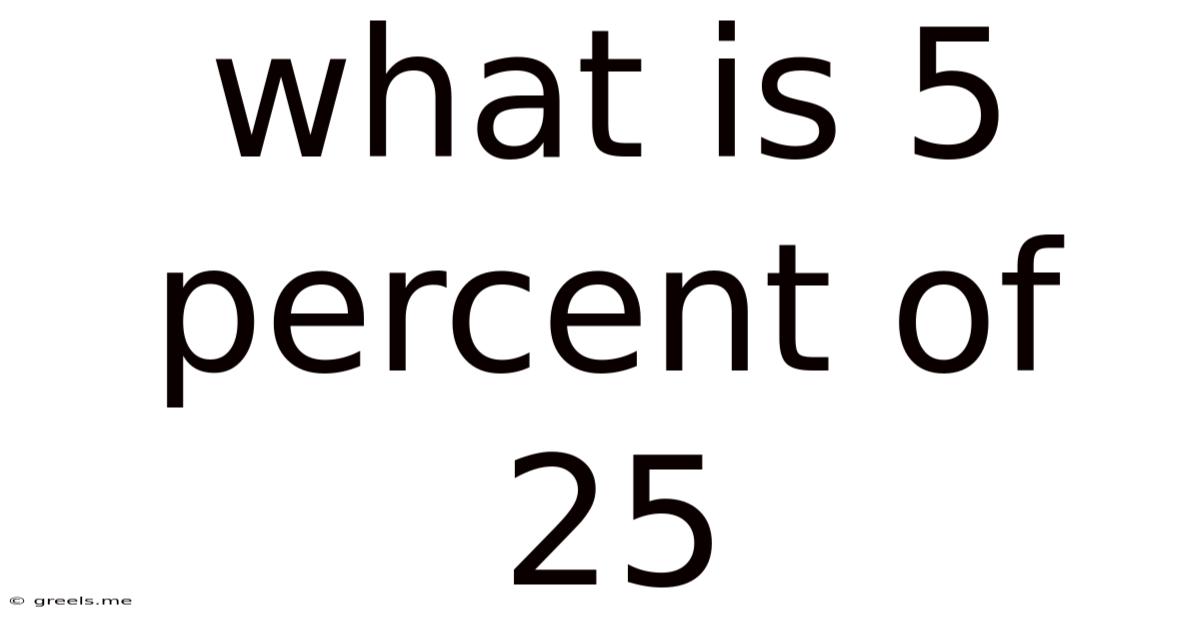
Table of Contents
What is 5 Percent of 25? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 5 percent of 25?" opens the door to a broader understanding of percentages, their practical applications, and how to calculate them efficiently. While the answer itself is straightforward, exploring the underlying concepts provides valuable insights for various real-world scenarios. This article will delve into the calculation, explain the methodology, explore different approaches, and discuss the relevance of percentages in various fields.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 5 percent means 5 out of every 100, or 5/100. This fraction can be simplified to 1/20. Understanding this fundamental concept is crucial for tackling any percentage calculation.
Calculating 5 Percent of 25: The Basic Method
The most straightforward way to calculate 5 percent of 25 is to convert the percentage to a decimal and then multiply it by the number.
-
Convert the percentage to a decimal: 5 percent is equivalent to 5/100 = 0.05
-
Multiply the decimal by the number: 0.05 * 25 = 1.25
Therefore, 5 percent of 25 is 1.25.
Alternative Methods: Different Approaches for the Same Result
While the above method is the most common, other approaches can be used, depending on the context and preference.
Method 2: Using Fractions
As mentioned earlier, 5 percent is equivalent to the fraction 1/20. Therefore, we can calculate 5 percent of 25 as follows:
(1/20) * 25 = 25/20 = 1.25
This method emphasizes the fractional representation of percentages and is useful when dealing with simpler percentages that have easy-to-handle fractional equivalents.
Method 3: Proportion Method
This method utilizes the concept of proportionality. We set up a proportion:
5/100 = x/25
Solving for 'x' (which represents 5 percent of 25), we cross-multiply:
100x = 5 * 25 100x = 125 x = 125/100 = 1.25
This method is particularly helpful in understanding the proportional relationship between percentages and the whole number.
Method 4: Using a Calculator
Most calculators have a percentage function. Simply input "25 * 5%", and the calculator will directly output 1.25. This method is quick and efficient, especially for more complex percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, calculating a 5% discount on a $25 item directly uses the concept we've explored.
-
Statistics: Percentages are used to represent data proportions, such as the percentage of a population with certain characteristics or the percentage change in a given variable over time. Understanding these percentages is critical for interpreting statistical data.
-
Science: In scientific studies, percentages are often used to express the concentration of solutions, the rate of reaction, or the error in measurements. For example, expressing the purity of a chemical sample.
-
Everyday Life: Percentages are encountered in everyday situations, such as calculating tips in restaurants, understanding sales discounts, or interpreting nutritional information on food labels. For instance, knowing that a product is 5% off helps us to make informed purchase decisions.
-
Business: Businesses use percentages extensively in sales, marketing, budgeting, and financial forecasting. Analyzing profit margins, comparing sales data from different periods, and predicting future trends all rely on percentage-based calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 5 percent of 25 is relatively simple, more complex percentage problems may involve finding the percentage, the whole number, or a combination of both. These scenarios require slightly more intricate calculations but still rely on the fundamental principles we've discussed.
Example 1: Finding the Percentage
If 1.25 is 5% of a certain number, what is that number?
This problem requires us to work backwards. We can set up an equation:
0.05 * x = 1.25
Solving for x:
x = 1.25 / 0.05 = 25
Therefore, 1.25 is 5% of 25.
Example 2: Finding the Whole Number
If 2.5 is 10% of a certain number, what is that number?
Again, we set up an equation:
0.10 * x = 2.5
Solving for x:
x = 2.5 / 0.10 = 25
Therefore, 2.5 is 10% of 25.
Example 3: Compound Percentages
Compound percentages involve calculating a percentage of a number, then calculating a percentage of the resulting number, and so on. These types of calculations are frequently encountered in financial contexts, particularly when dealing with interest that compounds over time. For example, calculating the value of an investment after several years with compound interest.
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Start with simple problems and gradually move towards more complex ones.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying concepts of percentages, fractions, and decimals. This understanding will enable you to adapt your approach to different problem types.
-
Use Visual Aids: Diagrams and charts can help to visualize percentage relationships and make calculations easier to comprehend.
-
Utilize Online Resources: Several online calculators and resources can assist with percentage calculations, allowing you to verify your results and explore different approaches.
Conclusion: The Significance of Percentage Calculations in a Data-Driven World
The simple calculation of 5 percent of 25 reveals a fundamental mathematical concept with wide-ranging applications. From everyday financial transactions to sophisticated scientific analyses, percentages are an indispensable tool for understanding and interpreting quantitative information. Mastering percentage calculations is not merely a mathematical skill; it's a crucial component of effective problem-solving and data analysis in a world increasingly driven by data. This deep dive into percentages has hopefully highlighted their importance and provided a comprehensive guide to calculating them effectively, enabling you to confidently tackle a wide range of percentage-related problems in various contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.