What Is 5 Percent Of 2000
Greels
Mar 26, 2025 · 5 min read
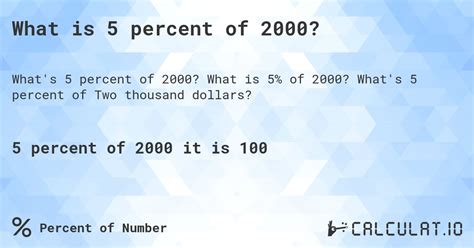
Table of Contents
What is 5 Percent of 2000? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting to complex financial analyses. Understanding how to determine a percentage of a number is crucial for making informed decisions and interpreting data effectively. This article will explore the simple calculation of "What is 5 percent of 2000?" and then delve into the broader context of percentages, their significance, and practical applications.
Calculating 5 Percent of 2000: The Basics
The most straightforward method for calculating 5 percent of 2000 is to convert the percentage into a decimal and then multiply it by the number. Here's how:
-
Convert the percentage to a decimal: 5 percent is equivalent to 5/100, which simplifies to 0.05.
-
Multiply the decimal by the number: 0.05 * 2000 = 100
Therefore, 5 percent of 2000 is 100.
This simple calculation can be easily performed using a calculator or even mentally for those familiar with percentage shortcuts. However, understanding the underlying principles is essential for tackling more complex percentage problems.
Beyond the Calculation: Understanding Percentages
Percentages are a way of expressing a proportion or fraction as a number out of 100. They provide a standardized way to compare different quantities and are widely used in various fields, including:
- Finance: Calculating interest rates, discounts, profits, and losses.
- Statistics: Representing data in charts and graphs, calculating probabilities.
- Retail: Determining discounts and sales prices.
- Science: Expressing concentrations, yields, and error margins.
- Everyday life: Understanding tax rates, tips, and more.
Understanding percentages allows you to analyze data, make comparisons, and interpret information more effectively. For example, knowing that a product is 20% off helps you assess its value compared to its original price. Similarly, understanding interest rates allows you to make informed decisions about borrowing or investing money.
Different Methods for Calculating Percentages
While the decimal method is the most common and efficient for most calculations, there are alternative approaches, particularly useful for mental calculations or when dealing with specific percentages:
-
Fraction Method: 5% can be expressed as the fraction 5/100. Therefore, 5% of 2000 can be calculated as (5/100) * 2000 = 100. This method is helpful for simple percentages that have easy-to-handle fraction equivalents.
-
Proportion Method: This method sets up a proportion to solve for the unknown value. For example:
x/2000 = 5/100
Cross-multiplying and solving for x gives us x = 100. This method can be helpful in understanding the relationship between the percentage and the whole.
-
Using a Calculator: Calculators offer the most convenient and accurate method for calculating percentages, especially with more complex calculations involving multiple percentages or larger numbers.
Practical Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world scenarios. Here are some examples:
1. Retail Discounts and Sales
Imagine a shirt originally priced at $2000 is on sale for 5% off. Using the knowledge gained above, you know the discount is $100, meaning the final price is $2000 - $100 = $1900.
2. Financial Calculations: Interest and Returns
Understanding percentage calculations is crucial for managing personal finances. If you invest $2000 and earn a 5% return, your profit will be $100. Similarly, understanding interest rates on loans allows you to compare different financing options.
3. Tax Calculations
Many countries use a percentage-based tax system. If the sales tax is 5%, and you purchase an item for $2000, the tax amount would be $100, bringing the total cost to $2100.
4. Tip Calculations
Calculating tips in restaurants often involves percentages. A 5% tip on a $2000 bill would be $100.
5. Statistical Analysis
In statistics, percentages are used to represent proportions within a larger dataset. For example, if 5% of 2000 survey respondents answered "yes" to a particular question, it represents 100 respondents. This allows for easier interpretation and comparison of data.
6. Scientific Applications
In scientific fields, percentages are frequently used to express concentrations, yields, or error margins. For instance, a 5% concentration of a solution implies that 5 out of every 100 units are the solute.
Advanced Percentage Calculations: Beyond the Basics
While the calculation of 5% of 2000 is relatively straightforward, more complex situations might arise involving multiple percentages, percentage increases/decreases, and compound interest.
Calculating Percentage Increase/Decrease
If a quantity increases by 5%, it's not simply adding 5%. You need to calculate the 5% increase and add it to the original amount. For example, a 5% increase on 2000 would be 100, resulting in a new value of 2100. A 5% decrease would involve subtracting 100 from 2000, resulting in 1900.
Compound Interest
Compound interest involves earning interest not only on the principal amount but also on accumulated interest. This leads to exponential growth over time. Understanding compound interest is crucial for long-term financial planning and investment strategies.
Multiple Percentages
Situations involving multiple percentages require sequential calculations. For instance, applying a 5% discount followed by a 10% tax would require calculating the discount first, then calculating the tax on the discounted amount. This order matters and gives a different final result than applying the tax first then the discount.
Conclusion: Mastering Percentages for a Brighter Future
Calculating percentages, even a seemingly simple calculation like finding 5% of 2000, forms the foundation for a deeper understanding of numerical relationships and data interpretation. This skill extends far beyond basic arithmetic, providing valuable tools for navigating financial decisions, interpreting statistics, and understanding various aspects of the world around us. By mastering the concept of percentages and exploring its numerous applications, we equip ourselves with a powerful toolset for making informed decisions and achieving our goals. From simple everyday tasks to complex financial analysis, the ability to confidently calculate and interpret percentages is an invaluable asset. Therefore, continuous practice and exploration of different percentage-related problems are highly encouraged to achieve proficiency in this area.
Latest Posts
Latest Posts
-
What Is 140 Cm In Inches
Mar 29, 2025
-
112 Inches Is How Many Feet
Mar 29, 2025
-
How Many Kilograms Is 37 Pounds
Mar 29, 2025
-
250 Grams Is How Many Pounds
Mar 29, 2025
-
Cuanto Es 146 Libras En Kg
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
