What Is 5 Percent Of 120
Greels
May 21, 2025 · 5 min read
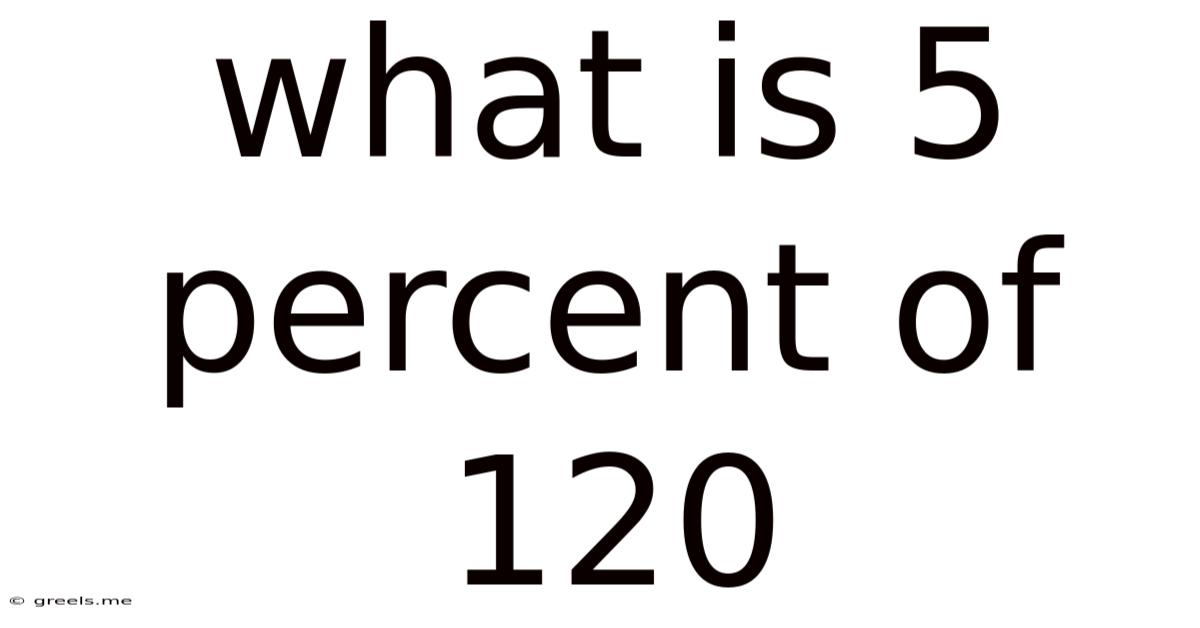
Table of Contents
What is 5 Percent of 120? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only answer the question, "What is 5 percent of 120?" but will also provide a comprehensive understanding of percentages, their calculation methods, and practical examples demonstrating their real-world utility.
Understanding Percentages
A percentage is a fraction or ratio expressed as a part of one hundred. The term "percent" is derived from the Latin phrase "per centum," meaning "out of one hundred." Percentages are represented by the symbol "%" and are used to express proportions, rates, and changes in various quantities. For example, 5% means 5 out of 100, or 5/100.
Calculating 5 Percent of 120
The most straightforward method to calculate 5 percent of 120 is to convert the percentage to a decimal and then multiply it by the number.
-
Step 1: Convert the percentage to a decimal: To convert 5% to a decimal, divide 5 by 100: 5 ÷ 100 = 0.05
-
Step 2: Multiply the decimal by the number: Multiply the decimal (0.05) by 120: 0.05 x 120 = 6
Therefore, 5 percent of 120 is 6.
Alternative Calculation Methods
While the above method is the most common, there are alternative ways to calculate percentages:
-
Using Fractions: 5% can be expressed as the fraction 5/100. To find 5% of 120, multiply 120 by 5/100: (5/100) x 120 = 6. This method highlights the fractional nature of percentages.
-
Using Proportions: You can set up a proportion: 5/100 = x/120. Cross-multiplying gives 100x = 600, and solving for x gives x = 6. This method is particularly useful when dealing with more complex percentage problems.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 120 x 5 %, and the calculator will automatically perform the calculation and display the result as 6.
Real-World Applications of Percentages
Percentages are ubiquitous in various aspects of daily life and professional fields:
1. Finance and Budgeting:
-
Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations is crucial for managing personal finances and making informed investment decisions. For example, calculating the interest accrued on a savings account or the total cost of a loan including interest requires percentage calculations.
-
Taxes: Taxes, such as sales tax, income tax, and property tax, are expressed as percentages. Knowing how to calculate percentages is crucial for determining the amount of tax payable and planning one's budget accordingly. Calculating the tax on a purchase or the tax refund you are due requires proficiency in percentage calculations.
-
Discounts and Sales: Retailers frequently offer discounts and sales expressed as percentages. Calculating the discounted price of an item requires understanding percentage reductions. For instance, a 20% discount on a $100 item means a $20 reduction, resulting in a final price of $80.
-
Investment Returns: Investors use percentages to track the performance of their investments. Calculating the percentage return on an investment helps assess its profitability. For instance, a 10% return on a $1000 investment means a profit of $100.
2. Science and Statistics:
-
Data Representation: Percentages are extensively used in scientific research and statistics to represent data proportions and trends. For example, expressing the percentage of respondents who answered "yes" to a survey question provides a concise summary of the data.
-
Error Analysis: Percentages are used to express error margins and confidence intervals in scientific experiments and data analysis. Understanding percentage error is crucial for interpreting the reliability and precision of experimental results.
-
Growth Rates: In biological studies, population growth rates and decay rates are often expressed as percentages. Calculating percentage growth or decline is important for modeling and predicting population dynamics.
3. Everyday Life:
-
Tips and Gratuities: Calculating tips in restaurants or other service industries often involves determining a percentage of the total bill. A common tip is 15% or 20% of the bill amount.
-
Shopping and Sales: As mentioned earlier, understanding percentages is crucial for determining the final price of items after discounts and sales. This helps make informed purchasing decisions and save money.
-
Cooking and Baking: Recipes often specify ingredients as percentages of the total weight or volume. Accurate percentage calculations ensure proper ingredient proportions and successful cooking results.
4. Business and Management:
-
Profit Margins: Businesses calculate their profit margins as percentages of revenue to assess their profitability and efficiency. A higher profit margin indicates a greater profitability.
-
Market Share: Market share, the proportion of a market controlled by a particular company or product, is expressed as a percentage. Monitoring market share helps companies assess their competitiveness.
-
Growth Projections: Businesses use percentages to project future growth in sales, revenue, and market share. Accurate percentage projections are vital for strategic planning and decision-making.
Advanced Percentage Calculations
While calculating 5% of 120 is relatively straightforward, more complex percentage problems might require multiple steps. For instance:
-
Calculating percentage increase or decrease: This involves finding the difference between two numbers and expressing it as a percentage of the original number.
-
Calculating percentage points: Percentage points refer to the arithmetic difference between two percentages, not a percentage change.
-
Compounding percentages: This involves applying a percentage repeatedly over time, such as calculating compound interest.
Mastering these advanced percentage calculations is crucial for various applications, including financial analysis, investment strategies, and economic forecasting.
Conclusion
Calculating 5 percent of 120, which equals 6, is a simple yet fundamental concept with vast implications. A deep understanding of percentages and their calculation methods is crucial for navigating various aspects of daily life, professional careers, and academic pursuits. From managing personal finances to interpreting scientific data and making informed business decisions, percentages provide a powerful tool for understanding proportions, rates, and changes in various quantities. The ability to confidently calculate and interpret percentages is a valuable skill that enhances decision-making and problem-solving capabilities across numerous fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.