What Is 40 Percent Of 3000
Greels
May 23, 2025 · 5 min read
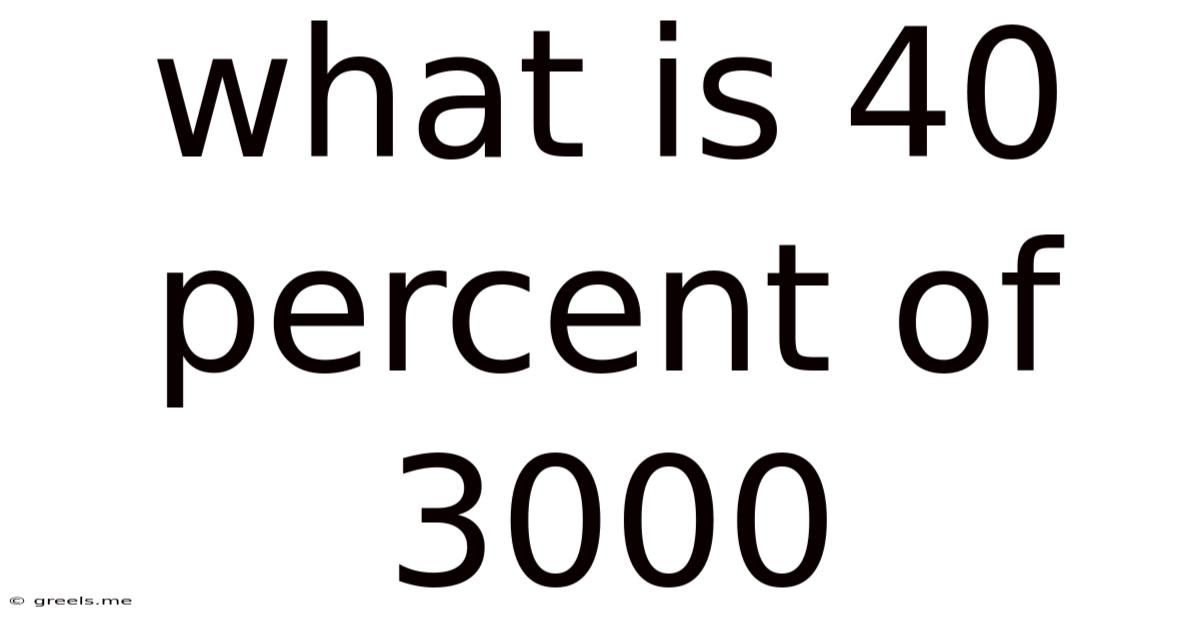
Table of Contents
What is 40 Percent of 3000? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to calculate percentages efficiently and accurately is crucial for making informed decisions and solving problems effectively. This article will comprehensively explore the calculation of "What is 40 percent of 3000?", providing not just the answer but also a detailed explanation of the underlying methods, real-world applications, and advanced techniques related to percentage calculations.
Understanding Percentages
Before diving into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. Essentially, a percentage represents a portion of a whole. For instance, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Calculating 40% of 3000: The Methods
There are several ways to calculate 40% of 3000. We'll explore the most common and straightforward methods:
Method 1: Using the Decimal Equivalent
This is perhaps the most common and efficient method. We convert the percentage to its decimal equivalent by dividing it by 100. Then, we multiply the decimal by the number.
- Step 1: Convert the percentage to a decimal: 40% / 100 = 0.40
- Step 2: Multiply the decimal by the number: 0.40 * 3000 = 1200
Therefore, 40% of 3000 is 1200.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 40% can be written as 40/100, which simplifies to 2/5. We can then use this fraction to calculate the percentage.
- Step 1: Express the percentage as a fraction: 40% = 40/100 = 2/5
- Step 2: Multiply the fraction by the number: (2/5) * 3000 = 1200
Again, the result is 1200.
Method 3: Using Proportions
Proportions offer another approach. We set up a proportion where x represents the unknown value (40% of 3000):
- Step 1: Set up the proportion: 40/100 = x/3000
- Step 2: Cross-multiply: 40 * 3000 = 100 * x
- Step 3: Solve for x: 120000 = 100x => x = 120000 / 100 = 1200
This method also yields the answer 1200.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world scenarios:
Finance and Budgeting:
- Calculating interest: Understanding interest rates and calculating the interest earned on savings or the interest paid on loans involves percentage calculations.
- Discounts and sales tax: Determining the final price of an item after a discount or adding sales tax requires calculating percentages.
- Investment returns: Calculating the return on investment (ROI) relies heavily on percentage calculations.
- Budgeting: Allocating a certain percentage of your income to different expenses (rent, food, entertainment, etc.) necessitates percentage calculations.
Business and Commerce:
- Profit margins: Calculating the profit margin of a product or service involves determining the percentage of profit relative to the cost.
- Market share: Businesses track their market share—the percentage of the total market they control—to gauge their performance.
- Sales growth: Businesses analyze sales growth by comparing current sales to previous sales as a percentage change.
- Pricing strategies: Companies use percentage-based pricing strategies to set prices for their products and services.
Science and Statistics:
- Data analysis: Percentages are frequently used to represent proportions within datasets and communicate statistical findings.
- Probability: Probability calculations frequently involve percentages.
- Experimental results: In scientific experiments, percentages are used to represent the success or failure rates of various outcomes.
Everyday Life:
- Tipping in restaurants: Calculating tips based on a percentage of the bill.
- Understanding nutrition labels: Food labels often display nutritional information as percentages of recommended daily values.
- Comparing prices: Comparing prices of different items requires calculating percentage differences.
- Understanding sales and discounts: Determining the savings from sales and discounts involves calculating percentages.
Advanced Percentage Calculations
Beyond the basic calculations, several more advanced techniques exist:
Percentage Change:
This is used to compare two numbers and express the change as a percentage. The formula is:
((New Value - Old Value) / Old Value) * 100
For example, if sales increased from 1000 to 1200, the percentage change is:
((1200 - 1000) / 1000) * 100 = 20%
Percentage Point Difference:
This is used to compare two percentages directly. It represents the absolute difference between two percentages, not a relative change. For instance, if the unemployment rate went from 5% to 8%, the percentage point difference is 3 percentage points (8% - 5% = 3%).
Compound Interest:
Compound interest is interest calculated not only on the principal but also on the accumulated interest from previous periods. This leads to exponential growth. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Reverse Percentage Calculations:
Sometimes, you might know the result after a percentage increase or decrease and need to find the original value. This requires working backward using algebraic techniques.
For example, if an item costs $120 after a 20% increase, the original price can be found using:
Let x be the original price. Then, x + 0.20x = 120. Solving for x, we get x = $100.
Conclusion: Mastering Percentage Calculations
Understanding and mastering percentage calculations is a valuable skill with wide-ranging applications. From everyday financial decisions to complex scientific analyses, the ability to calculate and interpret percentages is crucial for success in various fields. By utilizing the methods outlined above and exploring the more advanced techniques, you can confidently tackle a diverse range of percentage-related problems and make informed decisions based on accurate calculations. Remember that practice is key to mastering these concepts and building your confidence in working with percentages. The simple calculation of "What is 40 percent of 3000?" serves as a springboard to understanding this fundamental mathematical concept and its significant role in our daily lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 40 Percent Of 3000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.