What Is 3 Percent Of 8
Greels
May 22, 2025 · 5 min read
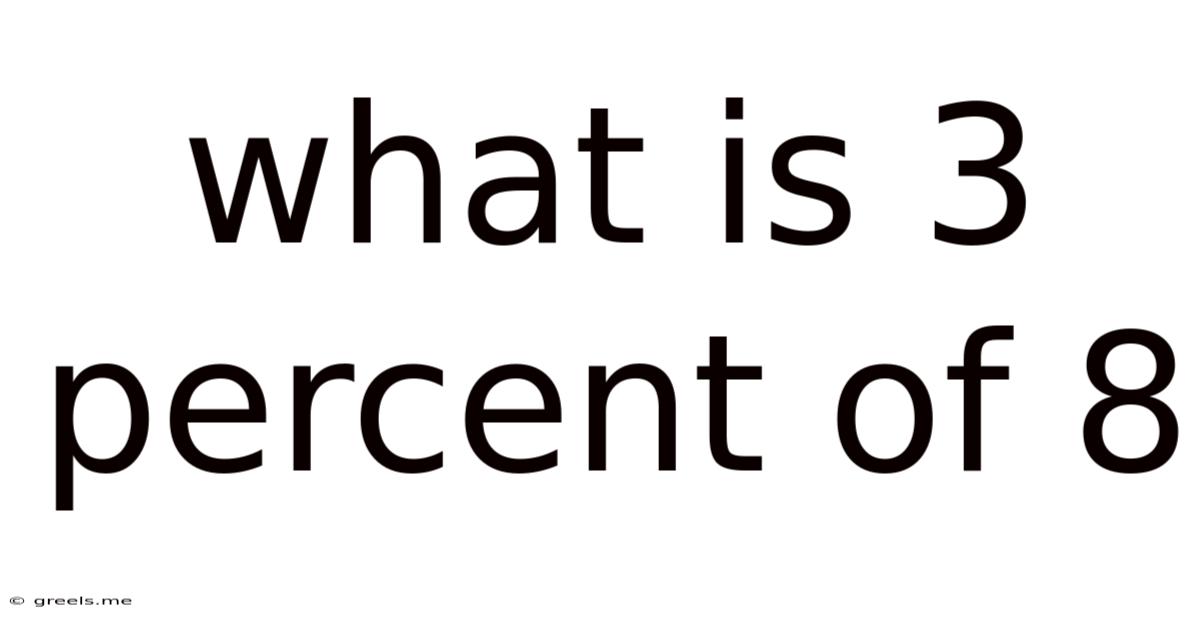
Table of Contents
What is 3 Percent of 8? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 3 percent of 8?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward – 0.24 – understanding the underlying principles and exploring the various contexts in which percentage calculations are used reveals a richer understanding of this fundamental mathematical operation. This article will not only answer the initial question but will also delve into the methods for calculating percentages, explore real-world examples, and discuss the importance of percentage calculations in various fields.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." Therefore, 3 percent (3%) means 3 out of every 100. This representation provides a standardized way to compare proportions and fractions, making it easier to understand and interpret data across various contexts.
Key Components of Percentage Calculations
Understanding the components involved in a percentage calculation is crucial. Every percentage problem involves three key elements:
- The Percentage: This is the rate or proportion expressed as a percentage (e.g., 3%).
- The Whole (or Base): This is the total amount or the value you are finding a percentage of (e.g., 8).
- The Part: This is the result of the percentage calculation, representing a portion of the whole (e.g., 0.24, which is 3% of 8).
Calculating 3 Percent of 8: Two Methods
There are two primary methods to calculate 3 percent of 8:
Method 1: Using the Decimal Equivalent
This method involves converting the percentage to its decimal equivalent and then multiplying it by the whole number.
- Convert the percentage to a decimal: To convert 3% to a decimal, divide it by 100: 3% / 100 = 0.03.
- Multiply the decimal by the whole number: Multiply the decimal equivalent (0.03) by the whole number (8): 0.03 * 8 = 0.24.
Therefore, 3 percent of 8 is 0.24.
Method 2: Using the Fraction Equivalent
This method involves converting the percentage to a fraction and then multiplying it by the whole number.
- Convert the percentage to a fraction: 3% can be written as the fraction 3/100.
- Multiply the fraction by the whole number: Multiply the fraction (3/100) by the whole number (8): (3/100) * 8 = 24/100.
- Simplify the fraction (if necessary) and convert to a decimal: 24/100 simplifies to 6/25, which is equal to 0.24.
Therefore, 3 percent of 8 is 0.24. Both methods yield the same result, highlighting the interconnectedness of decimals and fractions.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life and across various professional fields. Here are a few examples:
Finance and Investing
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding percentage calculations is crucial for managing personal finances effectively and making informed investment decisions.
- Stock Market: Percentage changes in stock prices are frequently reported to indicate gains or losses. Analyzing these percentage changes helps investors track portfolio performance and make strategic decisions.
- Taxes: Taxes are often levied as a percentage of income or the value of goods and services. Calculating tax amounts requires a thorough understanding of percentage calculations.
- Discounts and Sales: Retailers use percentages to advertise discounts and sales, allowing consumers to calculate the final price of goods after a percentage reduction.
Science and Research
- Data Analysis: Percentages are fundamental in analyzing data sets, particularly in scientific research. They are used to represent proportions, frequencies, and probabilities within larger datasets. For instance, researchers might report the percentage of participants in a study who exhibited a particular characteristic.
- Statistical Inference: Percentage-based calculations are essential in hypothesis testing and other statistical procedures commonly used in scientific research and analysis.
Everyday Life
- Tip Calculations: When dining out, calculating tips involves determining a percentage of the total bill. This practical application of percentage calculations ensures fair compensation for service.
- Sales Tax: Sales taxes are usually added to the price of goods and services as a percentage. Understanding this helps consumers accurately calculate the final price they will pay.
- Grocery Shopping: Comparing unit prices of different products often involves calculating percentages to determine the best value for money.
Advanced Applications: Compound Interest and Percentage Change
While the calculation of 3% of 8 is a simple example, the principles extend to more complex calculations:
Compound Interest
Compound interest involves earning interest on both the principal amount and accumulated interest. Understanding percentage calculations is crucial for calculating the total amount after a period of compounding. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Percentage Change
Percentage change is used to express the relative change between two values. It is calculated as:
Percentage Change = [(New Value - Old Value) / Old Value] x 100
This formula is used extensively to track changes in various metrics, such as population growth, economic indicators, and sales figures.
Conclusion: The Significance of Percentage Calculations
The seemingly simple question, "What is 3 percent of 8?" serves as a gateway to understanding the broader implications and applications of percentage calculations. From basic everyday calculations to complex financial modeling and scientific research, percentages provide a universal language for expressing proportions and facilitating comparisons. Mastering percentage calculations is a fundamental skill with far-reaching benefits across various aspects of life, both personal and professional. The ability to quickly and accurately calculate percentages enhances financial literacy, improves data interpretation skills, and ultimately contributes to more informed decision-making in diverse contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.