What Is 3 Percent Of 200
Greels
May 22, 2025 · 5 min read
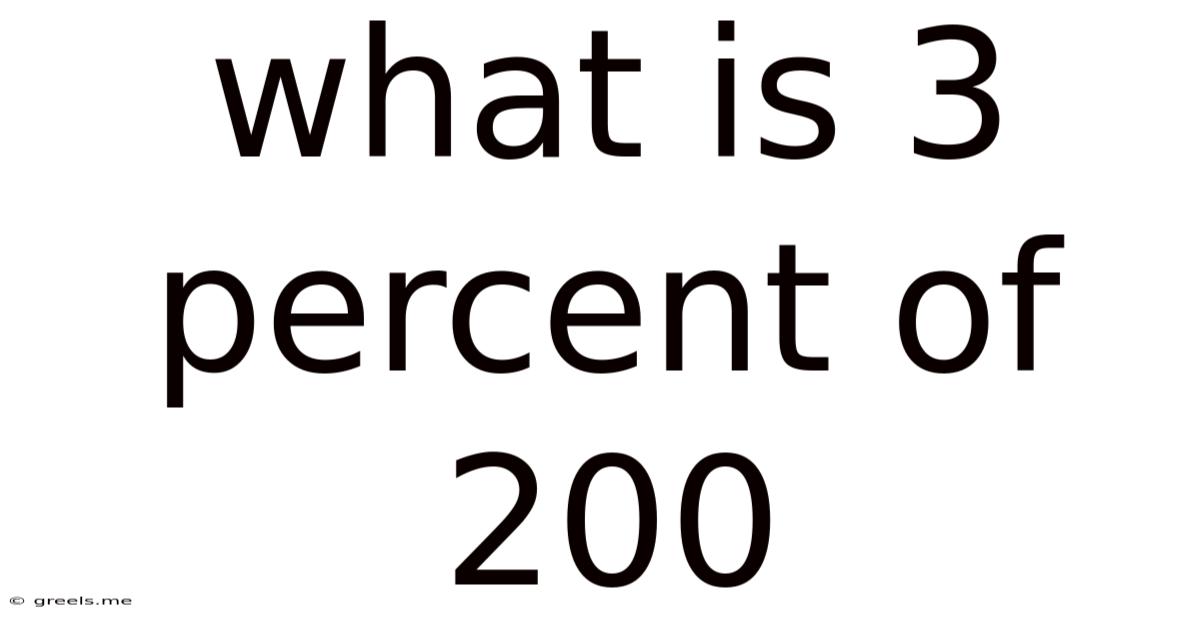
Table of Contents
What is 3 Percent of 200? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to calculate percentages empowers you to make informed decisions, interpret data effectively, and solve problems across diverse domains. This article explores the simple calculation of "What is 3 percent of 200?" and then delves deeper into the underlying concepts, practical applications, and advanced techniques related to percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." The symbol "%" is used to represent percentages. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5 as a decimal.
Calculating 3% of 200: The Simple Method
The most straightforward way to calculate 3% of 200 is to convert the percentage to a decimal and then multiply it by the number.
-
Convert the percentage to a decimal: 3% is equivalent to 3/100 = 0.03.
-
Multiply the decimal by the number: 0.03 * 200 = 6
Therefore, 3% of 200 is 6.
Alternative Methods: Using Fractions
Alternatively, you can solve this using fractions:
-
Represent the percentage as a fraction: 3% can be written as 3/100.
-
Multiply the fraction by the number: (3/100) * 200 = 6
This method provides an alternative perspective and reinforces the fundamental understanding of percentages as fractions.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in numerous contexts:
1. Finance and Budgeting:
-
Interest rates: Banks and financial institutions use percentages to calculate interest on loans, savings accounts, and investments. Understanding percentage calculations is crucial for managing personal finances effectively. For example, calculating the interest accrued on a savings account or the total cost of a loan with interest.
-
Discounts and Sales: Retailers frequently advertise discounts as percentages. Calculating the actual price reduction after a percentage discount is a common task for consumers. Understanding percentage calculations helps to identify the best deals and compare prices effectively.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the total amount. Calculating the tax amount is crucial for accurate budgeting and financial planning.
-
Investment Returns: Investors track investment performance using percentages, calculating returns on investment (ROI) to evaluate the success of their investment strategies.
2. Science and Statistics:
-
Data analysis: Percentages are widely used to represent proportions and trends in data sets. Scientists and statisticians use percentages to communicate findings and draw conclusions from research. Examples include calculating the percentage of respondents agreeing with a survey question or the percentage change in a population over time.
-
Probability and Statistics: Percentages are essential in expressing probabilities and analyzing statistical data. For example, determining the likelihood of an event occurring or summarizing the distribution of a dataset.
3. Everyday Life:
-
Tips and Gratuities: Calculating tips in restaurants often involves expressing the tip as a percentage of the bill. This is a common application of percentage calculation in everyday life.
-
Shopping and Sales: As mentioned earlier, understanding percentage discounts is key to making informed purchasing decisions.
-
Recipe Scaling: Adjusting recipes to serve more or fewer people often involves scaling ingredients by a percentage.
Advanced Percentage Calculations:
Beyond the basics, several advanced percentage calculations are frequently encountered:
1. Calculating Percentage Increase or Decrease:
This involves determining the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100%
For example, if a price increases from $100 to $120, the percentage increase is:
((120 - 100) / 100) * 100% = 20%
2. Finding the Original Value After a Percentage Change:
If you know the new value and the percentage change, you can work backward to find the original value. This involves using algebraic manipulation of the percentage change formula.
3. Calculating Percentage Points:
Percentage points represent the absolute difference between two percentages, rather than the relative difference. For example, an increase from 10% to 15% is a 5-percentage-point increase, not a 50% increase. Understanding this distinction is crucial for accurate interpretation of data.
4. Compound Interest:
Compound interest involves earning interest on both the principal amount and accumulated interest. This calculation uses exponential growth formulas and is essential for understanding long-term investments and loan repayments.
Tips and Tricks for Efficient Percentage Calculations:
-
Memorize common percentages: Knowing the decimal equivalents of common percentages (e.g., 10%, 25%, 50%, 75%) can speed up calculations.
-
Use a calculator: For complex calculations or when accuracy is critical, use a calculator or spreadsheet software to ensure precision.
-
Break down complex calculations: Large or multi-step percentage calculations can be simplified by breaking them down into smaller, manageable steps.
-
Practice regularly: The best way to master percentage calculations is through regular practice and application in various contexts.
Conclusion: The Importance of Mastering Percentages
Mastering percentage calculations is a valuable skill that extends far beyond simple arithmetic. Its widespread applicability in finance, science, and everyday life makes it an essential tool for informed decision-making and problem-solving. By understanding the fundamental concepts and applying the techniques discussed in this article, you can confidently tackle a wide range of percentage-related challenges and enhance your analytical abilities in diverse settings. From budgeting to investment strategies, understanding percentages empowers you to navigate the numerical world with greater efficiency and accuracy. The seemingly simple question, "What is 3 percent of 200?" serves as a gateway to a deeper appreciation of the power and versatility of percentage calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.