What Is 25 Percent Of 180
Greels
May 28, 2025 · 5 min read
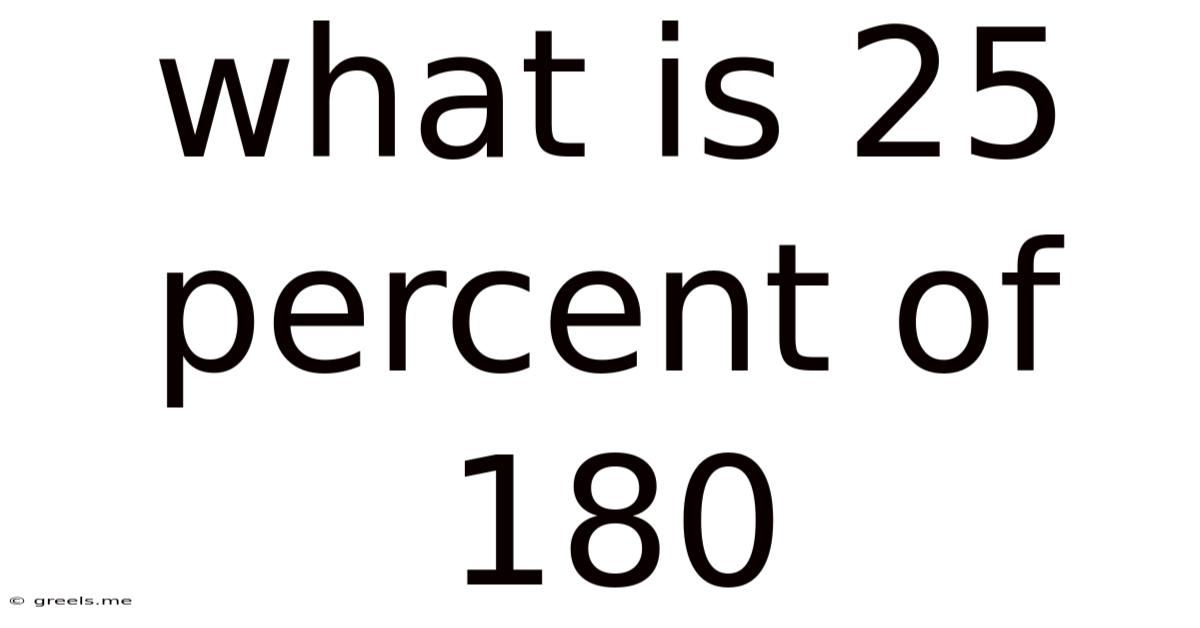
Table of Contents
What is 25 Percent of 180? A Deep Dive into Percentages and Their Applications
Finding 25% of 180 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics with broad real-world applications. This article will not only answer the question directly but will also delve into the various methods for calculating percentages, exploring their importance in different fields, and offering practical examples to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per cent). Therefore, 25% means 25 out of 100, which can be written as a fraction (25/100) or a decimal (0.25). Understanding this fundamental concept is key to tackling percentage calculations.
Key Percentage Relationships
Several key percentage relationships are crucial to remember:
- 50% = 1/2: Half of a number.
- 25% = 1/4: One-quarter of a number.
- 75% = 3/4: Three-quarters of a number.
- 10% = 1/10: One-tenth of a number.
- 1% = 1/100: One-hundredth of a number.
Knowing these relationships can often simplify calculations, allowing for mental arithmetic in many cases.
Calculating 25% of 180: Three Methods
There are several ways to calculate 25% of 180. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
Since 25% is equivalent to 1/4, we can calculate 25% of 180 by dividing 180 by 4:
180 / 4 = 45
Therefore, 25% of 180 is $\boxed{45}$.
Method 2: Converting to a Decimal
We can convert 25% to its decimal equivalent (0.25) and then multiply this decimal by 180:
0.25 * 180 = 45
This method is particularly useful when dealing with percentages that don't have simple fraction equivalents.
Method 3: Using Proportions
We can set up a proportion to solve for the unknown value (x):
25/100 = x/180
Cross-multiplying, we get:
100x = 25 * 180
100x = 4500
x = 4500 / 100
x = 45
Again, we find that 25% of 180 is $\boxed{45}$.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous real-world situations. Here are some examples:
1. Sales and Discounts
Percentage calculations are fundamental to understanding sales and discounts. If a store offers a 25% discount on an item priced at $180, you would save $45 (25% of $180). This knowledge empowers consumers to make informed purchasing decisions.
2. Finance and Investments
Percentages are vital in finance. Interest rates on loans and savings accounts are expressed as percentages. Calculating the interest earned or paid requires understanding percentage calculations. For example, a 5% interest rate on a $1000 investment would yield $50 in interest after one year. Understanding percentage growth and decay is also crucial for analyzing investment performance.
3. Statistics and Data Analysis
Percentages are widely used in presenting statistical data. For example, survey results often present data as percentages to show the proportion of respondents who answered in a particular way. Understanding percentages is critical for interpreting and drawing meaningful conclusions from data.
4. Taxes and Tax Rates
Tax rates are usually expressed as percentages. For example, a 10% sales tax on a $50 purchase would amount to $5 in tax. Accurate calculation of taxes requires a solid grasp of percentages.
5. Tip Calculations
Calculating tips in restaurants often involves percentages. A 15% tip on a $60 meal would be $9. The ability to quickly calculate tips is a useful skill in many social situations.
6. Grade Calculation
Many grading systems utilize percentages to represent a student's performance. For example, a score of 85% on a test indicates that a student correctly answered 85 out of 100 questions (or a proportional equivalent on a differently sized test).
7. Science and Engineering
Percentages play a significant role in various scientific and engineering disciplines. For example, calculating the efficiency of an engine or the concentration of a solution involves using percentages. Error rates in experiments are also often expressed as percentages.
Beyond the Basics: More Complex Percentage Problems
While calculating 25% of 180 is straightforward, more complex percentage problems may involve finding the percentage one number represents of another, or finding the original value before a percentage increase or decrease.
Finding the Percentage One Number Represents of Another
For example, if you earned $45 out of a possible $180 points on a test, what percentage did you earn? This involves setting up a proportion:
x/100 = 45/180
Solving for x, you find that you earned 25%.
Finding the Original Value After a Percentage Increase or Decrease
If an item is currently priced at $135 after a 25% increase, what was the original price? We can set up an equation:
Original Price * 1.25 = 135
Solving for the Original Price, we find it was $108.
Conclusion
The simple calculation of 25% of 180, resulting in 45, is a stepping stone to understanding the broader world of percentages. Their applications span diverse fields, impacting our daily lives from finances to shopping to education and beyond. Mastering percentage calculations is a valuable skill that enhances decision-making abilities and empowers us to navigate various numerical challenges effectively. By understanding the different methods of calculation and their practical applications, we can unlock a deeper understanding of this fundamental mathematical concept. From simple discounts to complex financial analyses, the ability to work with percentages is a highly transferable skill applicable in numerous professional and personal settings.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.