What Is 20 Percent Of 900
Greels
Apr 02, 2025 · 4 min read
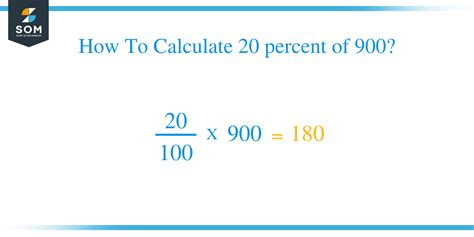
Table of Contents
What is 20 Percent of 900? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex business analyses. Understanding how to determine percentages not only empowers you to solve practical problems but also enhances your numerical literacy. This article delves into the calculation of "What is 20 percent of 900?", exploring different methods, providing step-by-step explanations, and illustrating the broader relevance of percentage calculations.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The symbol "%" signifies "per hundred." Therefore, 20% means 20 out of 100, which can also be expressed as the fraction 20/100 or the decimal 0.20.
Method 1: Using the Formula
The most straightforward method to calculate a percentage of a number involves a simple formula:
Percentage * Number = Result
In our case:
- Percentage: 20% or 0.20
- Number: 900
Applying the formula:
0.20 * 900 = 180
Therefore, 20% of 900 is 180.
Method 2: Fraction Conversion
Percentages can also be expressed as fractions. 20% is equivalent to 20/100, which simplifies to 1/5. Using this fractional representation, the calculation becomes:
(1/5) * 900 = 180
This method offers an alternative approach, highlighting the interchangeable nature of percentages and fractions.
Method 3: Proportions
Proportions provide another effective method for percentage calculations. We can set up a proportion to solve for the unknown value (x), representing 20% of 900:
20/100 = x/900
To solve for x, we cross-multiply:
20 * 900 = 100 * x
18000 = 100x
x = 18000 / 100
x = 180
This method reinforces the concept of proportional relationships and offers a more visual approach to solving percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-world scenarios. Consider these examples:
1. Financial Calculations:
- Discounts: Determining the discounted price of an item after a 20% sale.
- Taxes: Calculating the tax amount on a purchase.
- Interest: Computing interest earned on savings accounts or interest payable on loans.
- Tips: Calculating the appropriate tip amount in a restaurant.
- Investment Returns: Analyzing the return on investment (ROI) of financial assets.
2. Business and Economics:
- Profit Margins: Determining the percentage of profit earned on sales.
- Market Share: Analyzing a company's market share relative to competitors.
- Growth Rates: Calculating the percentage increase or decrease in sales, revenue, or other economic indicators.
- Inflation Rates: Understanding the impact of inflation on prices and purchasing power.
- Statistical Analysis: Employing percentages in various statistical measures, including mean, median, and mode.
3. Everyday Life:
- Recipe Scaling: Adjusting ingredient quantities in recipes.
- Grading: Converting numerical scores to percentages in academic settings.
- Surveys and Polls: Interpreting results expressed as percentages.
- Sales and Commission: Calculating sales commissions based on a percentage of sales.
- Comparison Shopping: Determining the best value for money based on price comparisons and percentage discounts.
Advanced Percentage Calculations: More Than Just the Basics
While calculating 20% of 900 is a relatively simple problem, understanding the underlying principles allows us to tackle more complex percentage calculations. Let's explore some advanced scenarios:
1. Calculating the Original Price After a Discount:
Imagine an item is on sale for $180 after a 20% discount. To find the original price, we can use the following approach:
Let x represent the original price. After a 20% discount, the remaining percentage is 80% (100% - 20%). Therefore:
0.80x = 180
x = 180 / 0.80
x = 225
The original price was $225.
2. Calculating Percentage Increase or Decrease:
Suppose a value increases from 900 to 1080. To calculate the percentage increase:
- Find the difference: 1080 - 900 = 180
- Divide the difference by the original value: 180 / 900 = 0.20
- Multiply by 100 to express as a percentage: 0.20 * 100 = 20%
The value increased by 20%.
Similarly, if a value decreases, the same process applies, but the result will be a negative percentage indicating a decrease.
3. Compound Percentage Changes:
Compound percentage changes involve applying a percentage change multiple times. For example, if a value increases by 10% and then by another 10%, the overall percentage increase is not simply 20%. The calculation involves applying each percentage change sequentially.
Using Technology for Percentage Calculations
While manual calculations are valuable for understanding the underlying principles, various technological tools simplify percentage calculations:
- Calculators: Most calculators include a percentage function that directly calculates percentages.
- Spreadsheets (e.g., Excel, Google Sheets): Spreadsheets offer formulas and functions for complex percentage calculations and data analysis.
- Online Percentage Calculators: Many websites offer online calculators specifically designed for percentage calculations.
Conclusion: The Ubiquity of Percentages
Understanding how to calculate percentages is a fundamental life skill with far-reaching implications. From managing personal finances and making informed purchasing decisions to analyzing business trends and interpreting statistical data, the ability to accurately and efficiently calculate percentages is essential for success in many aspects of life. This detailed exploration of calculating 20% of 900 and its various applications underscores the importance of mastering this crucial numerical skill. The various methods outlined here, from basic formulas to advanced calculations, empower you to confidently tackle any percentage problem you encounter. Remember to practice regularly, and you’ll quickly develop proficiency in this valuable skill.
Latest Posts
Latest Posts
-
How Many Kg Is 158 Lbs
Apr 03, 2025
-
How Many Mm In 9 5 Inches
Apr 03, 2025
-
How Many Grams Are In 2 5 Pounds
Apr 03, 2025
-
How Tall Is 38 Inches In Feet
Apr 03, 2025
-
How Many Kg Is 105 Pounds
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 900 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
