What Is 20 Percent Of 8
Greels
May 23, 2025 · 4 min read
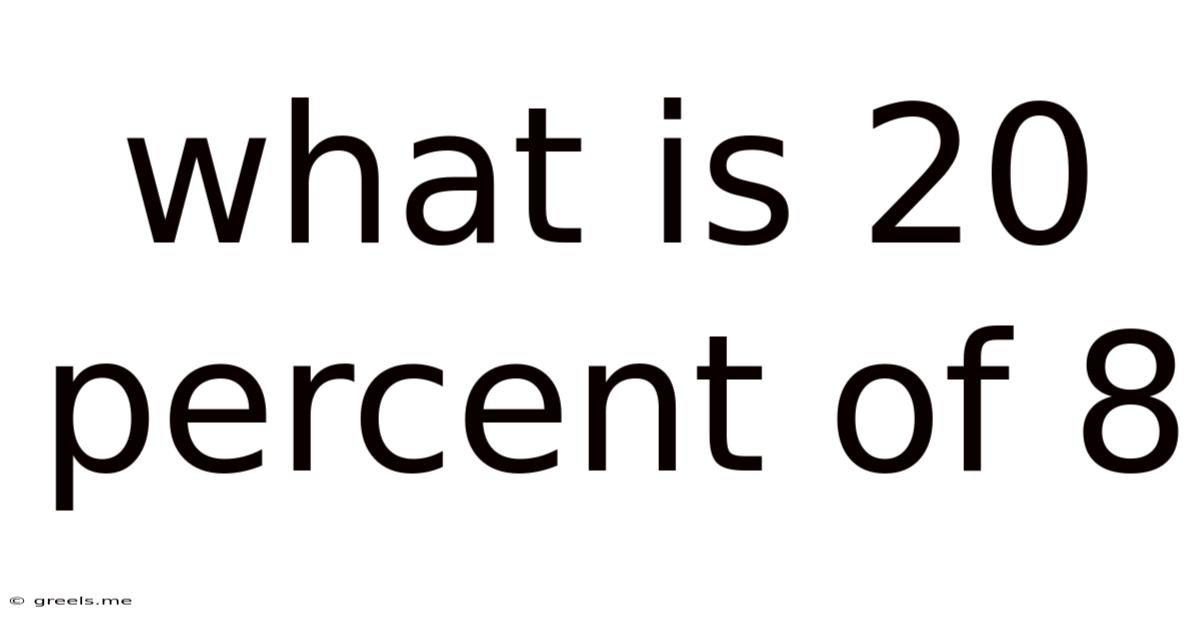
Table of Contents
What is 20 Percent of 8? A Deep Dive into Percentages and Their Applications
The question, "What is 20 percent of 8?" might seem deceptively simple. It's a basic percentage calculation, something many of us learned in elementary school. However, understanding this seemingly simple problem unlocks a world of applications across various fields, from everyday budgeting to complex financial modeling. This article will not only answer the question but delve into the underlying principles of percentages, exploring different methods of calculation and highlighting real-world examples where this type of calculation is crucial.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." This foundational concept is essential for understanding various mathematical and real-world scenarios. To represent a percentage, we use the "%" symbol.
For instance, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20. This representation is key to solving percentage problems.
Method 1: The Decimal Method – Calculating 20% of 8
This is the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
-
Convert the percentage to a decimal: 20% = 20/100 = 0.20
-
Multiply the decimal by the number: 0.20 * 8 = 1.6
Therefore, 20% of 8 is 1.6.
Method 2: The Fraction Method – An Alternative Approach
This method involves converting the percentage to a fraction and then multiplying.
-
Convert the percentage to a fraction: 20% = 20/100
-
Simplify the fraction (if possible): 20/100 simplifies to 1/5
-
Multiply the fraction by the number: (1/5) * 8 = 8/5 = 1.6
Again, 20% of 8 is 1.6.
Method 3: Using Proportions – A More Formal Approach
Proportions offer a structured way to solve percentage problems. We set up a proportion where we equate two ratios:
- One ratio represents the percentage (20/100)
- The other represents the unknown part (x/8), where 'x' is 20% of 8.
The proportion looks like this: 20/100 = x/8
To solve for 'x', we cross-multiply:
20 * 8 = 100 * x
160 = 100x
x = 160/100 = 1.6
Once again, 20% of 8 is 1.6.
Real-World Applications: Where Percentages Matter
The seemingly simple calculation of 20% of 8 has numerous real-world applications:
-
Sales and Discounts: Imagine a store offering a 20% discount on an item priced at $8. The discount amount would be $1.60. This is a fundamental calculation in retail and e-commerce. Understanding this allows consumers to quickly determine the final price after a discount. Businesses rely on accurate percentage calculations for profit margins and pricing strategies.
-
Taxes and Tips: Calculating sales tax or a tip in a restaurant often involves percentages. If the sales tax is 20% on an $8 item, the tax amount is $1.60. Similarly, leaving a 20% tip on an $8 meal would also be $1.60. These calculations are essential for managing personal finances and understanding the final cost of goods and services.
-
Interest Rates and Investments: Interest rates on loans and investments are expressed as percentages. If you invest $8 and earn a 20% annual interest, you'll gain $1.60 at the end of the year. This calculation is crucial for planning financial investments and understanding the returns on different investment options. Accurate percentage calculations are essential for making informed financial decisions.
-
Statistical Analysis: Percentages play a vital role in statistical analysis. They are frequently used to represent proportions, trends, and probabilities in data sets. For example, if a survey shows that 20% of 8 respondents prefer a particular product, this data helps businesses understand consumer preferences and make informed decisions about product development and marketing.
-
Scientific Research and Measurement: Percentages are used extensively in scientific research and experiments. They might represent the concentration of a substance, the success rate of an experiment, or the error margin in measurements.
-
Everyday Budgeting: Understanding percentages is fundamental for creating and managing personal budgets. Tracking expenses and allocating funds based on percentages (e.g., allocating 20% of income to savings) aids in financial planning and efficient resource management.
Beyond the Basics: Advanced Percentage Calculations
While the problem "What is 20% of 8?" focuses on finding a part of a whole, the concept of percentages extends to other calculations:
-
Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For example, if 1.6 is 20% of a number, what is the number?
-
Finding the Whole: If you know the part and the percentage, you can determine the whole. For example, if 1.6 represents 20% of a total, what is the total value?
These scenarios require slightly more complex calculations, often involving algebraic equations or the rearrangement of the percentage formula.
Conclusion: The Significance of a Simple Calculation
The answer to "What is 20% of 8?" is seemingly straightforward: 1.6. However, the importance of this simple calculation extends far beyond a single answer. Mastering this basic percentage calculation is a cornerstone to tackling more complex percentage-related problems that are frequently encountered in various aspects of life, from personal finance to professional endeavors. A strong understanding of percentages empowers individuals to make informed decisions, analyze data effectively, and navigate the numerical world with confidence. This seemingly small calculation opens a world of possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.