What Is 20 Percent Of 41
Greels
May 23, 2025 · 5 min read
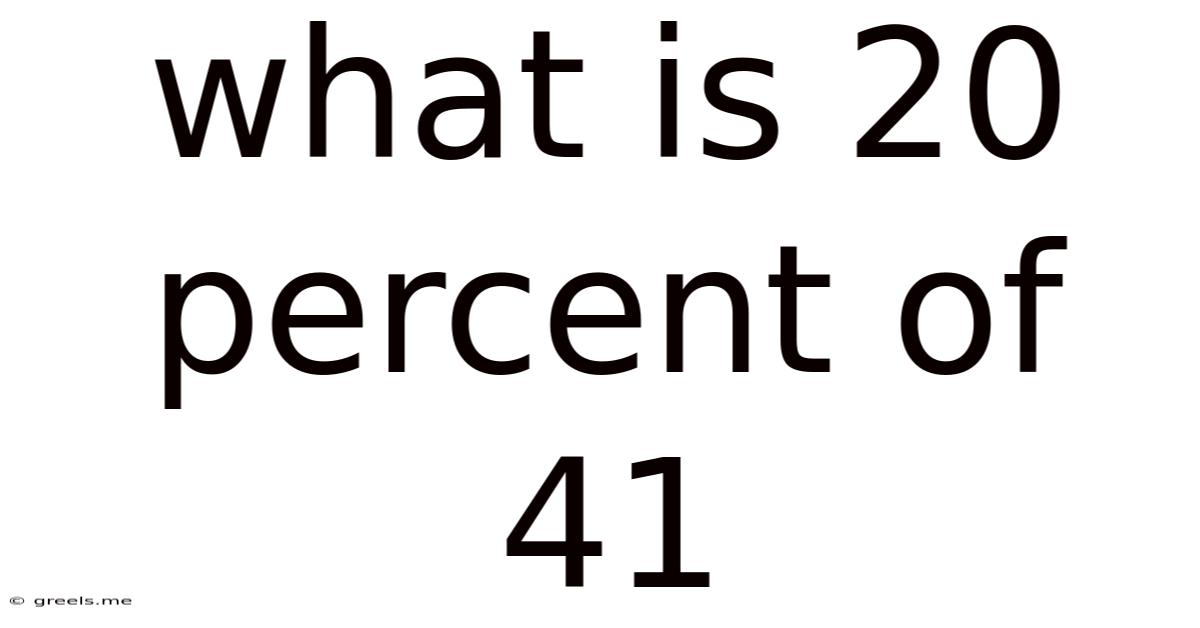
Table of Contents
What is 20 Percent of 41? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial modeling and scientific analysis. Understanding how to determine a percentage of a number is crucial for informed decision-making and problem-solving. This article will not only answer the question "What is 20 percent of 41?" but also explore the underlying concepts, different calculation methods, and real-world examples to solidify your understanding of percentages.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. This fraction represents a portion or proportion of a whole.
Key Concepts:
- Whole: This is the total amount or value you are considering. In our example, the whole is 41.
- Part: This is the portion of the whole you are interested in finding. We want to find 20% of 41, so the part is what we need to calculate.
- Percentage: This is the rate or proportion expressed as a fraction of 100. In our example, the percentage is 20%.
Calculating 20% of 41: Three Methods
There are several ways to calculate 20% of 41. Let's explore three common methods:
Method 1: Using the Fraction Method
Since 20% is equivalent to 20/100 or 1/5, we can calculate 20% of 41 as follows:
- Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Multiply the whole by the fraction: (1/5) * 41 = 8.2
Therefore, 20% of 41 is 8.2.
Method 2: Using Decimal Multiplication
This method involves converting the percentage to a decimal and then multiplying it by the whole number.
- Convert the percentage to a decimal: 20% = 20/100 = 0.20
- Multiply the whole by the decimal: 0.20 * 41 = 8.2
Again, we find that 20% of 41 is 8.2. This method is often preferred for its simplicity and ease of use with calculators.
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions to solve for the unknown part.
- Set up a proportion: Let 'x' represent 20% of 41. We can set up the proportion: 20/100 = x/41
- Cross-multiply: 100x = 20 * 41
- Solve for x: 100x = 820 => x = 820/100 = 8.2
This method reinforces the understanding of the relationship between the percentage, the part, and the whole. It's a valuable method, especially when dealing with more complex percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly versatile and finds its application in a wide array of situations:
1. Retail and Sales:
- Discounts: Stores frequently offer discounts like "20% off." Understanding percentage calculations allows consumers to quickly determine the actual price after the discount.
- Sales Tax: Calculating the sales tax on a purchase involves finding a percentage of the pre-tax price.
- Profit Margins: Businesses use percentages to track their profit margins – the percentage of revenue that represents profit.
2. Finance and Investments:
- Interest Rates: Calculating simple and compound interest on loans, savings accounts, and investments heavily relies on percentage calculations.
- Investment Returns: Tracking the percentage return on investments is essential for evaluating investment performance.
- Loan Payments: Determining monthly payments on loans, mortgages, and credit cards involves intricate percentage calculations.
3. Science and Statistics:
- Data Analysis: Percentages are used extensively in data analysis to represent proportions, trends, and variations in data sets.
- Probability and Statistics: Percentages are fundamental in expressing probabilities and statistical significance.
- Scientific Measurements: Expressing changes or variations in measurements often involves percentages.
4. Everyday Life:
- Tipping: Calculating a tip in a restaurant often involves finding a percentage of the bill.
- Budgeting: Allocating a percentage of your income to different expenses helps in creating a balanced budget.
- Grading: Many educational systems use percentages to represent grades and scores.
Beyond the Basics: Advanced Percentage Calculations
While calculating 20% of 41 is a straightforward example, percentage calculations can become more complex. Consider these scenarios:
- Calculating the percentage increase or decrease: This involves determining the percentage change between two values. For example, if a price increases from $41 to $50, the percentage increase can be calculated.
- Finding the original value after a percentage change: If you know the final value and the percentage change, you can work backward to find the original value.
- Dealing with multiple percentage changes: Successive percentage changes do not simply add up; understanding how they interact is crucial.
Mastering Percentages: Tips and Tricks
- Practice Regularly: The best way to master percentage calculations is through consistent practice. Solve various problems to build your confidence and understanding.
- Use Calculators Effectively: Calculators can greatly simplify the process, especially for more complex calculations. Learn to use your calculator's percentage function efficiently.
- Understand the Underlying Concepts: Focusing on the conceptual understanding of percentages, rather than just memorizing formulas, will aid in problem-solving.
- Break Down Complex Problems: For complex percentage problems, break them down into smaller, manageable steps.
Conclusion
Calculating 20% of 41, as we've demonstrated, is a relatively simple process, resulting in an answer of 8.2. However, the underlying concepts of percentages and their diverse applications are far-reaching. Mastering percentage calculations is not just about solving mathematical problems; it's about developing a crucial skill set applicable to various aspects of life, from personal finance to professional endeavors. By understanding the different methods of calculation and their real-world applications, you can effectively utilize percentages to make informed decisions and navigate the complexities of numerical data. Continuous practice and a solid grasp of the underlying principles are key to building your proficiency in this essential mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 41 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.