What Is 15 Percent Of 8
Greels
May 19, 2025 · 5 min read
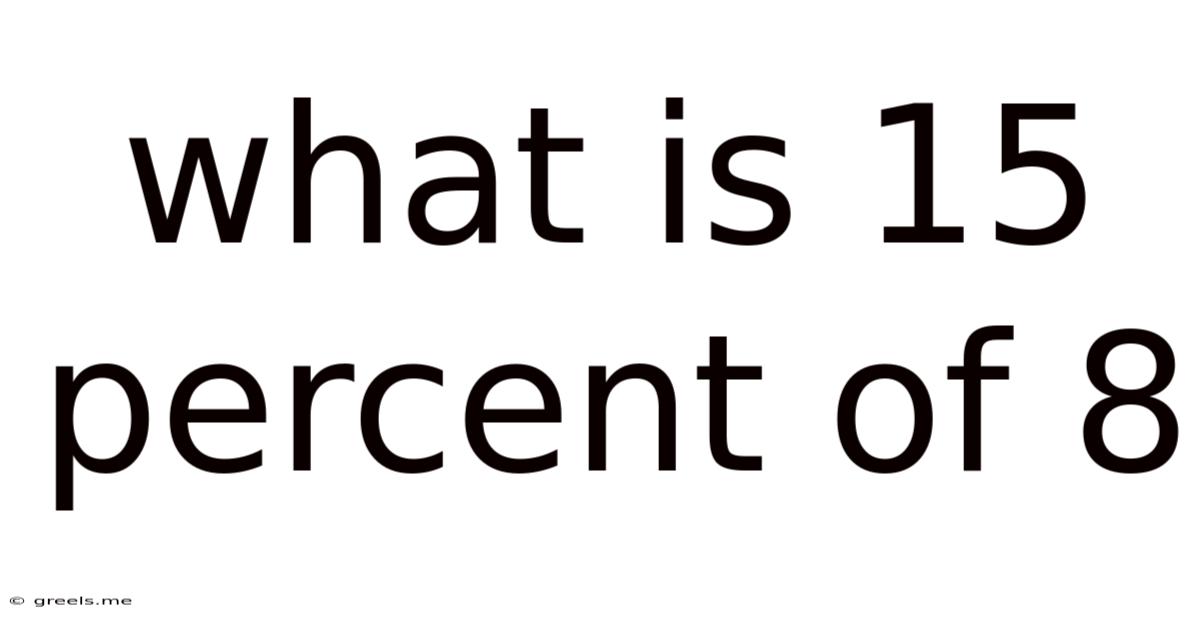
Table of Contents
What is 15 Percent of 8? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What is 15 percent of 8?", opens the door to a world of practical applications for percentage calculations. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to understanding financial reports and interpreting statistical data. This article will not only answer the question directly but also delve into the underlying mathematical concepts, provide multiple methods for solving similar problems, and explore real-world scenarios where this type of calculation is essential.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 15 percent (15%) means 15 out of 100, or 15/100. This can be represented as a decimal (0.15) or a fraction (15/100, which simplifies to 3/20).
This foundational understanding is key to tackling percentage calculations. Knowing that a percentage represents a proportion allows us to translate the problem into a solvable equation.
Calculating 15 Percent of 8: Three Methods
There are several ways to calculate 15 percent of 8. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward approach. First, convert the percentage to its decimal equivalent by dividing by 100:
15% ÷ 100 = 0.15
Then, multiply the decimal by the number you're finding the percentage of:
0.15 x 8 = 1.2
Therefore, 15 percent of 8 is 1.2.
Method 2: Using the Fraction Equivalent
We can also use the fraction equivalent of 15%. As we established, 15% is equal to 15/100, which simplifies to 3/20. To find 15% of 8, we multiply 8 by the fraction:
(3/20) x 8 = 24/20
Simplifying the fraction, we get:
24/20 = 6/5 = 1.2
Again, we arrive at the answer: 15 percent of 8 is 1.2.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between the percentage, the whole, and the part. We can set up a proportion:
15/100 = x/8
Where 'x' represents the unknown value (15% of 8). To solve for 'x', we cross-multiply:
15 x 8 = 100 x
120 = 100x
x = 120/100
x = 1.2
Once again, we confirm that 15 percent of 8 is 1.2.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a valuable life skill with numerous applications across various domains:
Finance and Budgeting:
- Discounts: Calculating discounts on sale items is a common application. If a $20 item is discounted by 15%, you'd calculate 15% of $20 to determine the discount amount.
- Taxes: Calculating sales tax or income tax involves percentage calculations. For instance, calculating 7% sales tax on a purchase requires finding 7% of the purchase price.
- Interest Rates: Understanding interest rates on loans, savings accounts, or investments relies heavily on percentage calculations. The interest earned or paid is typically a percentage of the principal amount.
- Investment Returns: Tracking investment performance involves calculating percentage returns or losses on investments.
Statistics and Data Analysis:
- Data Interpretation: Many statistical measures are expressed as percentages, such as percentages of respondents in surveys, or the percentage change in a particular data set over time.
- Probability: Probability is often expressed as a percentage, representing the likelihood of an event occurring.
- Data Visualization: Percentages are commonly used in charts and graphs to represent proportions and comparisons.
Everyday Life:
- Tips and Gratuities: Calculating a tip at a restaurant usually involves finding a percentage (e.g., 15% or 20%) of the bill.
- Recipe Adjustments: Adjusting recipes to serve more or fewer people often requires scaling ingredients by a percentage.
- Sales Commission: Salespeople often earn a commission based on a percentage of their sales.
Advanced Percentage Calculations
While the example of finding 15% of 8 is relatively simple, percentage calculations can become more complex, involving multiple percentages, consecutive percentage changes, or even percentage increases and decreases.
For example:
-
Consecutive Percentage Changes: Imagine a price increase of 10% followed by a 15% decrease. This wouldn't simply be a 5% net change; you'd need to calculate the percentages sequentially to determine the final price.
-
Finding the Percentage Increase or Decrease: Determining the percentage change between two numbers requires calculating the difference between the numbers, dividing it by the original number, and then multiplying by 100.
-
Finding the Original Value: If you know the percentage increase or decrease and the final value, you can work backward using algebraic equations to find the original value.
Mastering Percentage Calculations: Tips and Resources
Mastering percentage calculations requires practice and a strong understanding of the underlying concepts. Here are some helpful tips:
- Practice Regularly: Work through various problems, starting with simple examples and gradually increasing the complexity.
- Use Different Methods: Try all the methods discussed (decimal, fraction, proportion) to develop a versatile approach.
- Understand the Context: Pay close attention to the specific context of the problem to ensure you're applying the correct calculation.
- Use Online Calculators (for verification only): While it's crucial to understand the process, online calculators can be helpful for verifying your answers. However, always prioritize understanding the method over just using the calculator.
- Utilize Educational Resources: Plenty of online resources, textbooks, and educational videos offer comprehensive explanations and practice problems.
Conclusion
This in-depth exploration of calculating 15 percent of 8 has revealed that the answer is 1.2. More importantly, this simple problem has served as a gateway to understanding the wider world of percentage calculations. From everyday expenses to complex financial analysis, the ability to confidently and accurately perform percentage calculations is an invaluable skill for navigating various aspects of life, both personal and professional. By understanding the fundamental concepts, practicing different methods, and applying these skills in real-world contexts, you can effectively use percentages to solve a broad range of problems and make informed decisions.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.