What Is 15 Percent Of 2500
Greels
Apr 12, 2025 · 5 min read
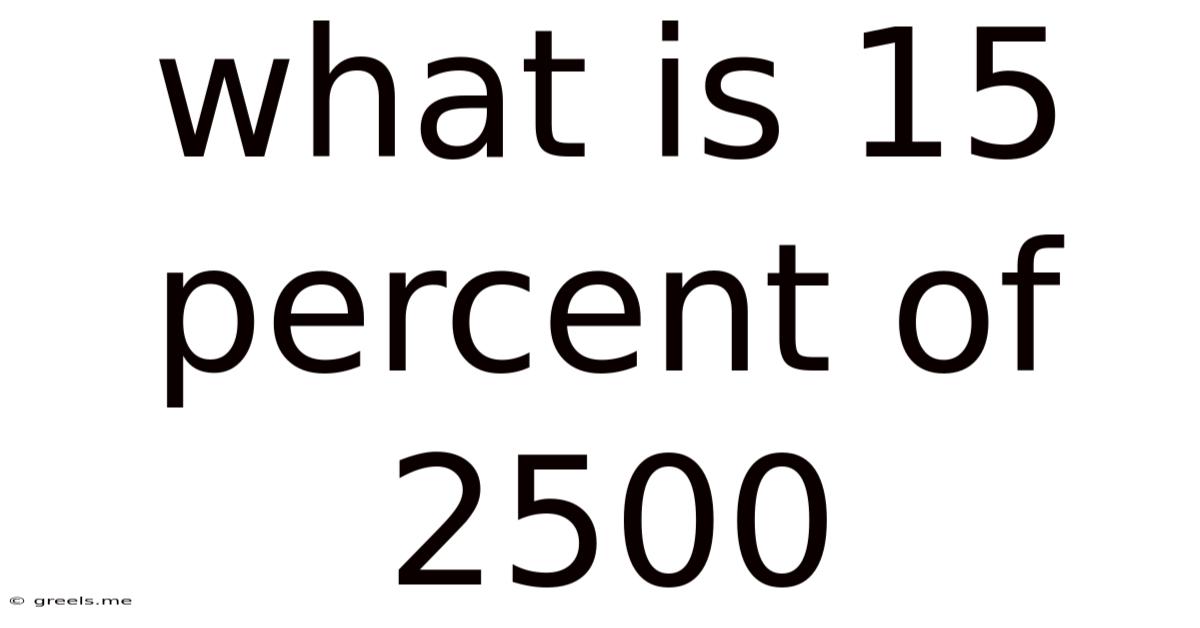
Table of Contents
What is 15 Percent of 2500? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various aspects of life, from financial planning and budgeting to understanding statistics and analyzing data. This article delves into the question, "What is 15 percent of 2500?", providing a step-by-step solution, exploring different calculation methods, and highlighting the practical applications of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" or "out of 100". For example, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15.
Calculating 15% of 2500: Method 1 - Using Decimal Conversion
The most straightforward method to calculate 15% of 2500 involves converting the percentage to a decimal and then multiplying it by the number.
Steps:
-
Convert the percentage to a decimal: Divide the percentage by 100. In this case, 15% / 100 = 0.15
-
Multiply the decimal by the number: Multiply 0.15 by 2500. 0.15 * 2500 = 375
Therefore, 15% of 2500 is 375.
Calculating 15% of 2500: Method 2 - Using Fraction Conversion
Alternatively, you can convert the percentage to a fraction and then multiply it by the number.
Steps:
-
Convert the percentage to a fraction: Express 15% as a fraction: 15/100
-
Simplify the fraction (if possible): The fraction 15/100 can be simplified by dividing both the numerator and the denominator by 5, resulting in 3/20.
-
Multiply the fraction by the number: Multiply 3/20 by 2500: (3/20) * 2500 = 7500/20
-
Simplify the result: Divide 7500 by 20: 7500 / 20 = 375
Therefore, 15% of 2500 is 375. Both methods yield the same result, demonstrating the equivalence between decimal and fractional representations of percentages.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world situations. Here are some examples:
1. Finance and Budgeting
- Calculating discounts: Retail stores frequently offer discounts expressed as percentages. Understanding percentage calculations allows you to quickly determine the final price after a discount. For instance, a 15% discount on a $2500 item is $375, resulting in a final price of $2125.
- Calculating interest: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating interest earned or paid requires knowledge of percentage calculations.
- Analyzing financial statements: Financial statements, such as income statements and balance sheets, utilize percentages extensively to represent ratios and proportions of various financial items. Analyzing these statements necessitates a solid understanding of percentages.
- Calculating taxes: Sales taxes, income taxes, and property taxes are often expressed as percentages. Calculating the amount of tax owed or the after-tax amount requires an understanding of percentage calculations.
2. Statistics and Data Analysis
- Understanding proportions: Percentages are used to represent proportions within datasets. For instance, a survey might reveal that 15% of respondents prefer a particular product.
- Interpreting data visualizations: Charts and graphs frequently utilize percentages to represent data visually, making it essential to understand their meaning and interpretation.
- Calculating probabilities: Probabilities are often expressed as percentages, representing the likelihood of an event occurring.
3. Everyday Life
- Calculating tips: Calculating a tip at a restaurant usually involves determining a percentage of the total bill.
- Understanding sales and promotions: Many sales and promotions are advertised using percentages, making it essential to calculate the savings.
- Comparing prices: Comparing the prices of different items requires understanding percentages to determine which offers the best value.
- Calculating increases and decreases: Percentage change calculations are used to quantify increases or decreases in various quantities over time. For example, if the price of an item increased from 2000 to 2500, the percentage increase is calculated as follows: [(2500-2000)/2000] * 100% = 25%.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 2500 is a straightforward example, percentage calculations can become more complex. Here are some scenarios that require slightly more advanced techniques:
- Finding the original amount: If you know the percentage and the resulting amount, you can calculate the original amount using algebraic equations. For example, if 15% of a number is 375, you can set up the equation: 0.15x = 375. Solving for x gives you the original number.
- Calculating percentage increase or decrease: These calculations require determining the difference between two numbers and expressing it as a percentage of the original number.
- Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest. These calculations are more complex than simple interest calculations.
- Working with multiple percentages: Some problems involve applying multiple percentages successively. For example, calculating the final price after a 10% discount followed by a 5% sales tax.
Mastering Percentage Calculations: Tips and Resources
To improve your percentage calculation skills, consider these tips:
- Practice regularly: The more you practice, the more proficient you'll become. Start with simple problems and gradually progress to more complex ones.
- Utilize online calculators: Many online calculators are available to check your answers and provide additional practice.
- Understand the underlying concepts: A strong understanding of fractions and decimals is essential for mastering percentage calculations.
- Break down complex problems: If a problem seems overwhelming, break it down into smaller, more manageable steps.
Conclusion
Calculating 15% of 2500, which equals 375, is a simple yet fundamental percentage calculation with wide-ranging applications. Mastering percentage calculations is crucial for success in various fields, from finance and statistics to everyday life. By understanding the methods and applying the tips mentioned, you can confidently tackle percentage problems and make informed decisions in numerous situations. Remember to practice regularly and explore additional resources to further enhance your skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 2500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.