What Is 15 Percent Of 200
Greels
Mar 31, 2025 · 5 min read
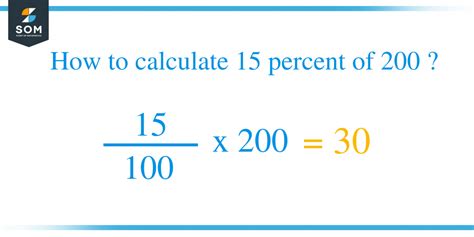
Table of Contents
What is 15 Percent of 200? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. This article will not only answer the question "What is 15 percent of 200?" but also delve into the underlying principles of percentage calculations, providing you with a comprehensive understanding and equipping you with the skills to tackle similar problems with ease.
Understanding Percentages: The Basics
A percentage is simply a fraction or a ratio expressed as a part of 100. The term "percent" literally means "per hundred." When we say 15 percent, we mean 15 out of every 100, which can be written as the fraction 15/100 or the decimal 0.15.
Understanding this fundamental concept is crucial to mastering percentage calculations. Every percentage problem can be translated into a simple equation involving fractions or decimals.
Calculating 15 Percent of 200: Three Methods
There are several ways to calculate 15 percent of 200. Let's explore three common methods:
Method 1: Using the Fraction Method
This method involves converting the percentage to a fraction and then multiplying it by the number.
-
Convert the percentage to a fraction: 15% is equal to 15/100.
-
Multiply the fraction by the number: (15/100) * 200
-
Simplify the equation: Notice that 200/100 simplifies to 2. The equation becomes 15 * 2.
-
Calculate the result: 15 * 2 = 30
Therefore, 15 percent of 200 is 30.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying it by the number.
-
Convert the percentage to a decimal: 15% is equal to 0.15 (move the decimal point two places to the left).
-
Multiply the decimal by the number: 0.15 * 200
-
Calculate the result: 0.15 * 200 = 30
Again, we arrive at the answer: 15 percent of 200 is 30.
Method 3: Using the Proportion Method
This method sets up a proportion to solve for the unknown value.
-
Set up a proportion: We can express the problem as a proportion: x/200 = 15/100, where 'x' represents 15% of 200.
-
Cross-multiply: 100x = 15 * 200
-
Solve for x: 100x = 3000 => x = 3000/100
-
Calculate the result: x = 30
Once again, we find that 15 percent of 200 is 30.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in a wide array of situations. Here are a few examples:
1. Retail Sales and Discounts
Imagine a store offering a 15% discount on a $200 item. Using the methods outlined above, you can quickly calculate the discount amount ($30) and the final price ($170). This is a crucial skill for savvy shoppers.
2. Calculating Taxes
Sales tax, income tax, and other taxes are often expressed as percentages. Knowing how to calculate percentages allows you to determine the tax amount on purchases or income.
3. Financial Planning and Investments
Percentage calculations are fundamental in financial planning and investment analysis. Calculating interest earned on savings accounts, returns on investments, and loan payments all rely on understanding percentages.
4. Scientific and Statistical Analysis
Percentages are widely used in scientific research and statistical analysis to represent proportions, changes, and probabilities. For example, researchers might express the percentage of participants in a study who responded positively to a treatment.
5. Everyday Budgeting
Budgeting effectively often requires tracking expenses as percentages of income. Knowing the percentage of your income spent on housing, food, or transportation can help you make informed decisions about your finances.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 200 is relatively straightforward, more complex percentage problems may involve finding the percentage, the original number, or the percentage increase or decrease. Let's explore these scenarios:
Finding the Percentage
If you know the original number (200) and the resulting number (30), you can find the percentage by dividing the resulting number by the original number and multiplying by 100: (30/200) * 100 = 15%.
Finding the Original Number
If you know the percentage (15%) and the resulting number (30), you can find the original number by dividing the resulting number by the percentage (as a decimal): 30 / 0.15 = 200.
Percentage Increase or Decrease
Percentage changes are often used to show how a value has changed over time. To calculate a percentage increase or decrease:
-
Find the difference: Subtract the original value from the new value.
-
Divide the difference by the original value: This gives you the decimal equivalent of the percentage change.
-
Multiply by 100: This converts the decimal to a percentage.
For example, if a value increases from 200 to 230, the percentage increase is: (30/200) * 100 = 15%.
Mastering Percentage Calculations: Tips and Tricks
Here are a few tips and tricks to help you master percentage calculations:
-
Practice regularly: The more you practice, the more comfortable and proficient you'll become.
-
Use a calculator: For more complex calculations, a calculator can save you time and effort. Many calculators have built-in percentage functions.
-
Understand the context: Pay close attention to the wording of the problem to ensure you understand what is being asked.
-
Break down complex problems: If a problem seems overwhelming, break it down into smaller, more manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: The Power of Percentage Calculations
As demonstrated throughout this article, understanding and mastering percentage calculations is a crucial skill with far-reaching applications. From everyday financial transactions to complex scientific analyses, the ability to accurately calculate percentages is essential for making informed decisions and solving a wide range of problems. By understanding the basic principles and practicing regularly, you can develop confidence and proficiency in this important mathematical skill. Remember, the answer to "What is 15 percent of 200?" is definitively 30, but the real value lies in understanding the underlying processes and their applications in your life.
Latest Posts
Latest Posts
-
How Many Inches Is 185 Mm
Apr 02, 2025
-
How Many Inches Is 152 Mm
Apr 02, 2025
-
How Many Feet In 112 Inches
Apr 02, 2025
-
How Many Inches In 114 Cm
Apr 02, 2025
-
26 Lbs Is How Many Kg
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
