What Is 15 Percent Of 150
Greels
Apr 03, 2025 · 4 min read
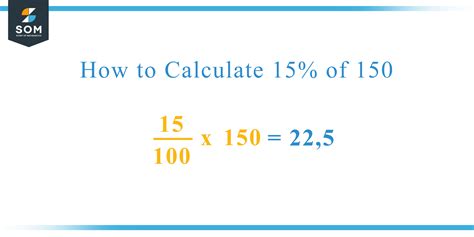
Table of Contents
What is 15 Percent of 150? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial modeling and scientific analysis. Understanding how to calculate percentages not only helps you solve specific problems but also fosters a deeper understanding of proportional relationships and numerical reasoning. This article will meticulously explore the question "What is 15 percent of 150?" and delve into the broader concepts of percentages, their calculation methods, and their practical uses.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, 15% can be interpreted as 15 parts out of 100, or 15/100. This fractional representation is crucial for understanding how to perform percentage calculations.
Key Concepts:
- The Whole: This is the total amount or value you're working with. In our case, the whole is 150.
- The Percentage: This is the portion of the whole you're interested in finding. Here, it's 15%.
- The Part: This is the result of the percentage calculation—the specific amount representing the percentage of the whole. This is what we aim to calculate.
Calculating 15 Percent of 150: Three Methods
There are several ways to calculate 15% of 150. Let's explore three common methods:
Method 1: Converting Percentage to Decimal
This is perhaps the most straightforward method. We convert the percentage to a decimal by dividing it by 100.
- Convert the percentage to a decimal: 15% / 100 = 0.15
- Multiply the decimal by the whole: 0.15 * 150 = 22.5
Therefore, 15% of 150 is 22.5.
Method 2: Using Fractions
This method utilizes the fractional representation of a percentage.
- Convert the percentage to a fraction: 15% = 15/100
- Simplify the fraction (optional): 15/100 simplifies to 3/20
- Multiply the fraction by the whole: (3/20) * 150 = 450/20
- Simplify the result: 450/20 = 22.5
Again, the answer is 22.5.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where x represents the unknown part:
15/100 = x/150
To solve for x, we cross-multiply:
15 * 150 = 100 * x 2250 = 100x x = 2250/100 x = 22.5
The result remains 22.5.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a wide array of scenarios:
1. Finance and Budgeting:
- Calculating interest: Understanding percentage calculations is essential for comprehending interest rates on loans, savings accounts, and investments.
- Analyzing financial statements: Businesses use percentages to analyze profit margins, expense ratios, and other key financial metrics.
- Calculating discounts and sales tax: Determining the final price of an item after a discount or adding sales tax involves percentage calculations.
- Budgeting and expense tracking: Individuals use percentages to track their spending and ensure they stay within their budget.
2. Retail and Sales:
- Calculating discounts: Retailers regularly offer discounts expressed as percentages. Calculating the discounted price requires percentage calculations.
- Analyzing sales performance: Businesses track sales figures and analyze sales growth using percentages.
- Calculating markups: Retailers determine the selling price of products by adding a markup percentage to the cost price.
3. Science and Statistics:
- Expressing data as percentages: Scientific studies frequently represent data as percentages to show proportions and trends.
- Calculating error margins: In scientific experiments, error margins are often expressed as percentages.
- Probability and statistics: Percentages are fundamental in calculating probabilities and interpreting statistical data.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants involves calculating a percentage of the bill.
- Understanding nutrition labels: Food labels often express nutrient content as percentages of the recommended daily intake.
- Comparing prices: Percentage calculations help compare the prices of different products and determine which offers the best value.
Beyond the Basics: Advanced Percentage Calculations
While calculating 15% of 150 is a straightforward example, percentage calculations can become more complex. Here are some examples of more advanced scenarios:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values. For example, if a value increases from 100 to 120, the percentage increase is 20%.
- Calculating percentage points: Percentage points represent the absolute difference between two percentages. For instance, an increase from 10% to 15% is a 5-percentage point increase.
- Solving for the original value: Given a percentage and the resulting value, you can calculate the original value. For example, if 20% of a number is 40, the original number is 200.
Conclusion: The Importance of Percentage Mastery
Understanding percentages is a vital life skill. The ability to perform percentage calculations confidently empowers you to make informed decisions in various contexts, from personal finance and shopping to professional endeavors and scientific pursuits. While calculating 15% of 150 might seem like a simple task, mastering this foundational skill opens the door to a deeper comprehension of numerical relationships and their implications in the real world. The methods outlined in this article—converting to decimals, using fractions, and employing proportions—provide a versatile toolkit for tackling various percentage problems, no matter how complex they may seem. By practicing these methods and applying them to real-world scenarios, you can build your numerical fluency and enhance your ability to navigate the quantitative aspects of everyday life.
Latest Posts
Latest Posts
-
What Is 32 Mm In Inches
Apr 04, 2025
-
What Day Was It 500 Days Ago
Apr 04, 2025
-
What Is 4 Percent Of 5000
Apr 04, 2025
-
155 Mm Is How Many Inches
Apr 04, 2025
-
How Many Kilograms Are In 22 Pounds
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
