What Is 15 Percent Of 14
Greels
May 20, 2025 · 4 min read
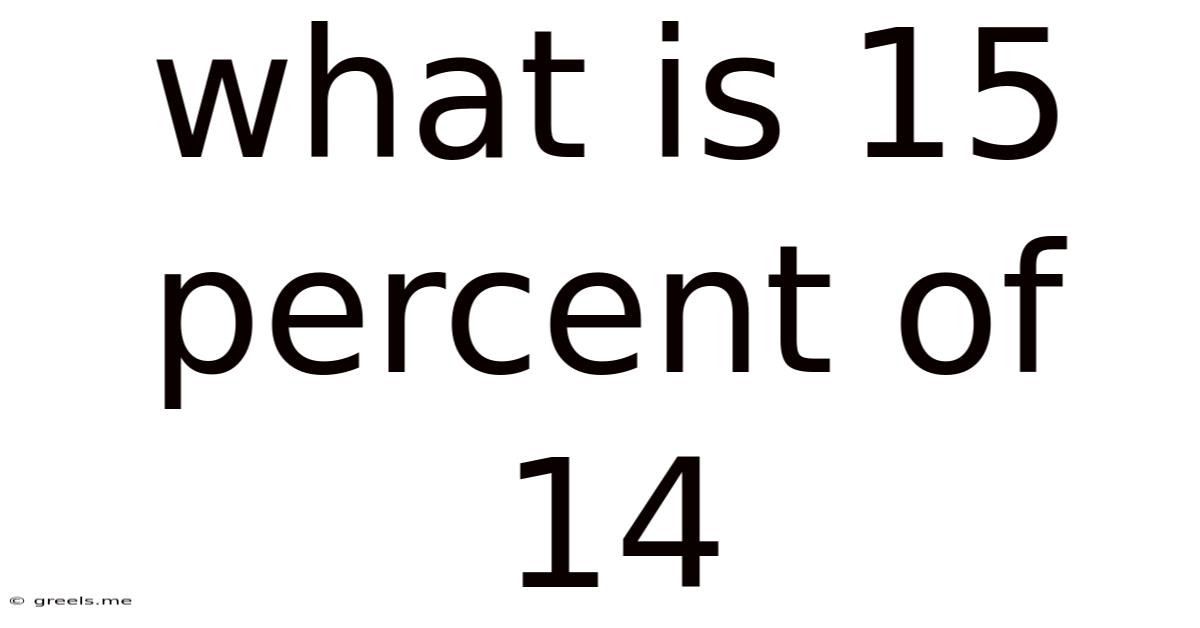
Table of Contents
What is 15 Percent of 14? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from finance and budgeting to sales and statistics. Understanding how to determine a percentage of a number is crucial for making informed decisions and interpreting data accurately. This article will meticulously explore the calculation of "what is 15 percent of 14," providing not only the answer but also a comprehensive understanding of the underlying principles and various methods for solving percentage problems. We'll also delve into practical applications and explore how to perform similar calculations quickly and efficiently.
Understanding Percentages
Before we dive into the specific calculation, let's establish a solid understanding of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 15% means 15 out of 100, or 15/100, which simplifies to 3/20 as a fraction and 0.15 as a decimal.
This fundamental understanding is key to solving any percentage problem. We can represent any percentage as a fraction or decimal, making it easier to perform the necessary calculations.
Method 1: Using the Formula
The most straightforward method to calculate a percentage of a number involves using a simple formula:
Percentage * Number = Result
In our case:
- Percentage: 15% = 0.15 (decimal representation)
- Number: 14
Therefore, the calculation is:
0.15 * 14 = 2.1
Therefore, 15 percent of 14 is 2.1
This method is highly efficient and easily adaptable to any percentage and number combination. Simply substitute the given values into the formula, and you'll obtain the desired result.
Method 2: Fraction Method
We can also solve this problem using fractions. As mentioned earlier, 15% can be expressed as the fraction 15/100. The calculation then becomes:
(15/100) * 14 = 210/100 = 2.1
This method provides a more visual representation of the calculation, clearly showing the fraction involved. Simplifying fractions before performing the multiplication can often make the calculation easier.
Method 3: Proportion Method
The proportion method offers a different perspective on solving percentage problems. It sets up a proportion using two equivalent ratios:
(Percentage/100) = (Result/Number)
Substituting our values:
(15/100) = (Result/14)
To solve for the Result, we cross-multiply:
15 * 14 = 100 * Result
210 = 100 * Result
Result = 210/100 = 2.1
This method, while slightly more involved, reinforces the concept of proportional relationships and offers another valuable approach to solving percentage problems.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is vital in numerous real-world scenarios. Here are a few examples:
- Finance: Calculating interest on loans, savings accounts, or investments. Understanding discounts and sales tax. Analyzing financial statements and budgets.
- Sales: Determining discounts, calculating commissions, and analyzing sales performance. Projecting future sales based on percentage growth.
- Statistics: Analyzing data sets, interpreting survey results, and understanding statistical significance. Calculating probabilities and proportions.
- Everyday Life: Determining tips in restaurants, calculating sale prices, and understanding percentage increases or decreases in prices or quantities.
Beyond the Basics: More Complex Percentage Problems
While the calculation "15 percent of 14" is relatively straightforward, many percentage problems require more intricate approaches. Let's briefly explore some of these complexities:
-
Calculating the Percentage Increase or Decrease: This involves finding the percentage change between two values. For example, determining the percentage increase in sales from one year to the next. The formula typically used involves finding the difference between the two values, dividing by the original value, and then multiplying by 100.
-
Finding the Original Value: Sometimes you know the result and the percentage, but need to find the original value. For example, if you received a 10% discount and paid $90, you would need to work backward to determine the original price.
-
Compound Percentages: These calculations involve applying a percentage multiple times, such as calculating compound interest or the effect of multiple discounts applied sequentially.
Tips and Tricks for Efficient Percentage Calculations
-
Mental Math: For simple percentages like 10%, 20%, or 50%, mental calculation is often faster. 10% is simply moving the decimal point one place to the left. 50% is halving the number.
-
Using a Calculator: For more complex percentages or when accuracy is paramount, a calculator is indispensable. Most calculators have a percentage function that simplifies the process.
-
Practice: The more you practice solving percentage problems, the more proficient you'll become. Start with simple examples and gradually progress to more complex calculations.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is an essential skill for navigating various aspects of life, from personal finance to professional pursuits. Understanding the fundamental principles, employing different calculation methods, and practicing regularly will significantly enhance your ability to solve percentage problems efficiently and accurately. The simple calculation of "15 percent of 14" serves as a foundational step towards mastering this critical skill and unlocking its wide-ranging applications. Remember to utilize the methods outlined in this article – the formula method, the fraction method, and the proportion method – to confidently tackle any percentage problem you encounter. Practice consistently and you will effortlessly navigate the world of percentages.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.