What Is 12.8 As A Fraction
Greels
May 03, 2025 · 4 min read
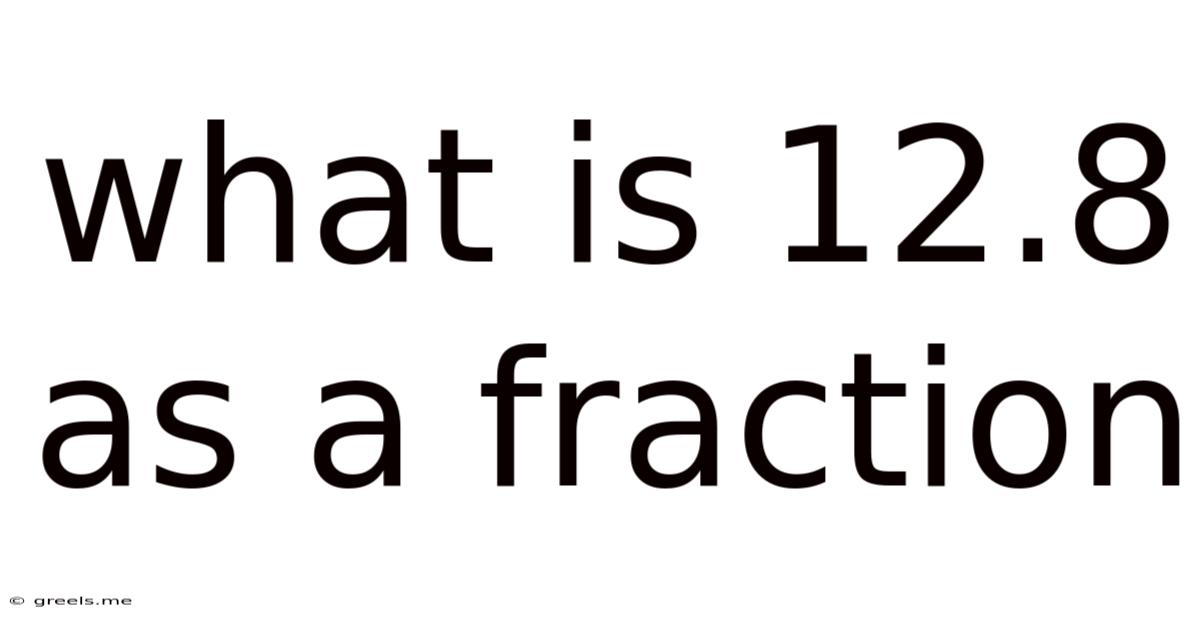
Table of Contents
What is 12.8 as a Fraction? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a structured approach, it becomes a straightforward process. This comprehensive guide will walk you through converting 12.8 into a fraction, explaining the underlying principles and providing you with the tools to tackle similar conversions with ease. We'll delve into the methodology, explore different approaches, and address common pitfalls to ensure a thorough understanding. This guide will be beneficial for students, educators, and anyone looking to sharpen their mathematical skills.
Understanding Decimals and Fractions
Before we embark on the conversion, let's briefly review the concepts of decimals and fractions.
Decimals represent parts of a whole using a base-ten system. The numbers to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, in 12.8, the '8' represents eight-tenths.
Fractions, on the other hand, express parts of a whole as a ratio of two integers – a numerator (top number) and a denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Converting 12.8 to a Fraction: Step-by-Step Guide
The conversion of 12.8 to a fraction involves several simple steps:
Step 1: Express the Decimal as a Fraction over 1
The first step is to write the decimal number as a fraction with a denominator of 1. This is a foundational step that simplifies the subsequent calculations.
12.8 = 12.8/1
Step 2: Remove the Decimal Point by Multiplying
To eliminate the decimal point, we need to multiply both the numerator and the denominator by a power of 10. The power of 10 is determined by the number of digits after the decimal point. In this case, there's one digit after the decimal (8), so we multiply by 10.
(12.8 x 10) / (1 x 10) = 128/10
Step 3: Simplify the Fraction
The fraction 128/10 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both 128 and 10 without leaving a remainder. In this case, the GCD of 128 and 10 is 2.
Dividing both the numerator and the denominator by 2, we get:
128/10 = (128 ÷ 2) / (10 ÷ 2) = 64/5
Step 4: Express as a Mixed Number (Optional)
While 64/5 is a perfectly acceptable fraction, we can also express it as a mixed number. A mixed number combines a whole number and a proper fraction. To do this, divide the numerator (64) by the denominator (5):
64 ÷ 5 = 12 with a remainder of 4
Therefore, 64/5 can be written as 12 4/5
Alternative Approach: Understanding Place Value
Another way to understand this conversion is by focusing on place value. The number 12.8 can be broken down as:
- 12: Represents 12 whole units.
- 0.8: Represents 8 tenths, which can be written as 8/10.
Combining these: 12 + 8/10 = 12 8/10
Simplifying 8/10 (by dividing both numerator and denominator by 2) gives us 4/5. Therefore, we arrive at the same result: 12 4/5.
Dealing with More Complex Decimal Conversions
The process outlined above can be applied to more complex decimal numbers. For instance, let's consider converting 3.14 to a fraction:
- Express as a fraction over 1: 3.14/1
- Multiply to remove the decimal: (3.14 x 100) / (1 x 100) = 314/100
- Simplify the fraction: The GCD of 314 and 100 is 2. Simplifying gives 157/50.
This demonstrates the adaptability of this method for handling various decimal numbers. Remember, the key is to multiply by the appropriate power of 10 to remove the decimal point and then simplify the resulting fraction to its lowest terms.
Common Mistakes to Avoid
When converting decimals to fractions, several common errors can occur:
- Incorrect multiplication: Failing to multiply both the numerator and denominator by the same power of 10 is a frequent mistake. This leads to an incorrect fraction.
- Improper simplification: Not simplifying the fraction to its lowest terms is another common error. Always find the GCD of the numerator and denominator and divide both by it.
- Misinterpreting place value: Misunderstanding the place value of digits after the decimal point can lead to incorrect initial fraction representation.
Practice Makes Perfect
The best way to master converting decimals to fractions is through consistent practice. Try converting various decimal numbers into fractions, focusing on understanding the steps involved. Start with simpler decimals and gradually move towards more complex ones. The more you practice, the more intuitive the process will become.
Conclusion
Converting 12.8 to a fraction, resulting in 64/5 or 12 4/5, involves a straightforward process of expressing the decimal as a fraction, multiplying to remove the decimal point, and simplifying the resulting fraction. Understanding the underlying principles of decimals and fractions, along with careful attention to detail, ensures accurate conversions. This process is applicable to a wide range of decimal numbers, allowing for consistent and reliable results. By mastering this skill, you enhance your mathematical proficiency and improve your ability to work with different numerical representations. Remember to practice regularly to reinforce your understanding and improve your speed and accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 12.8 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.