What Is 1 7 Of 42
Greels
May 03, 2025 · 5 min read
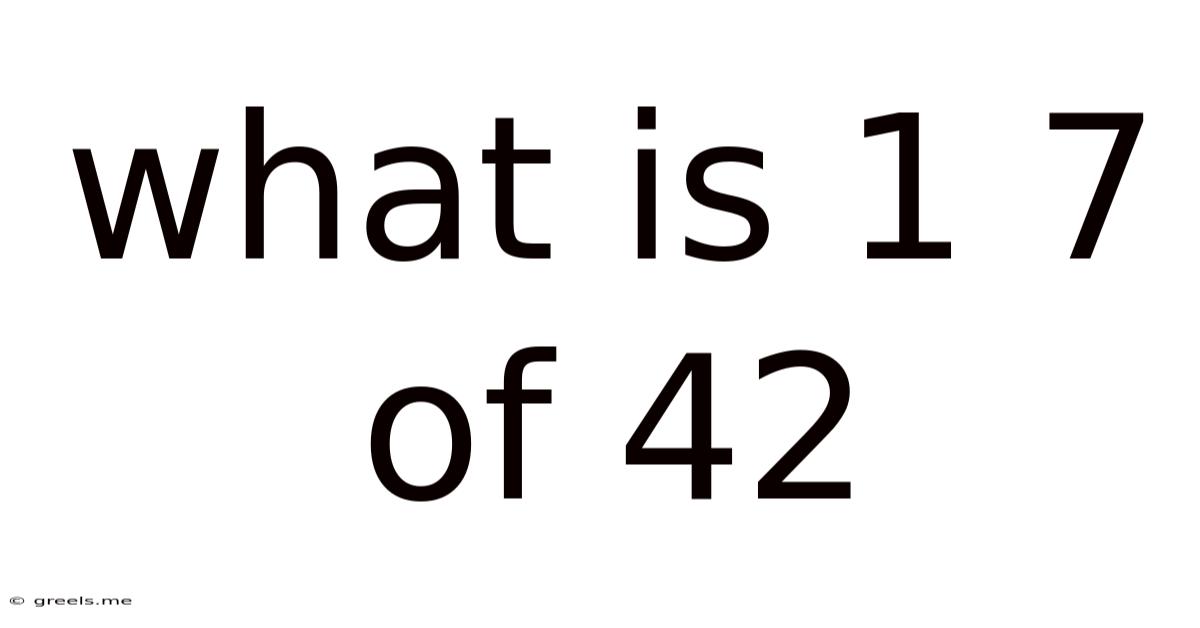
Table of Contents
What is 1/7 of 42? A Comprehensive Guide to Fractions and Their Applications
This seemingly simple question, "What is 1/7 of 42?", opens the door to a fascinating exploration of fractions, their significance in mathematics, and their practical applications in everyday life. While the answer itself is straightforward, understanding the underlying principles solidifies a crucial foundation in mathematical reasoning. This article will not only provide the solution but also delve into the conceptual understanding of fractions, different methods for solving similar problems, and showcase the widespread use of fractions in various fields.
Understanding Fractions: A Foundation in Mathematics
A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator specifies how many of those parts are being considered. In our case, 1/7 signifies one part out of seven equal parts.
Key Concepts to Remember:
- Numerator: The number above the fraction bar (1 in 1/7). It represents the number of parts we are interested in.
- Denominator: The number below the fraction bar (7 in 1/7). It represents the total number of equal parts the whole is divided into.
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 1/7, 3/4).
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator (e.g., 7/3, 5/5).
- Mixed Number: A combination of a whole number and a proper fraction (e.g., 1 2/3).
Calculating 1/7 of 42: Methods and Approaches
There are several ways to calculate 1/7 of 42. Let's explore the most common and effective methods:
Method 1: Direct Multiplication
The most straightforward method is to multiply the fraction (1/7) by the whole number (42):
(1/7) * 42 = 42/7
This results in an improper fraction. To simplify, we divide the numerator (42) by the denominator (7):
42 ÷ 7 = 6
Therefore, 1/7 of 42 is 6.
Method 2: Division First, then Multiplication
Alternatively, we can first divide 42 by the denominator (7) and then multiply the result by the numerator (1):
42 ÷ 7 = 6
6 * 1 = 6
This method provides the same result, highlighting the interchangeable nature of multiplication and division in fraction calculations.
Method 3: Visual Representation
For a visual understanding, imagine a whole divided into seven equal parts. Each part represents 1/7 of the whole. Since we have 42 in total, we can divide 42 into seven equal groups:
42 ÷ 7 = 6
Each group contains 6 units. Therefore, one of these groups (1/7) represents 6.
Practical Applications of Fractions in Real Life
Fractions are far from being abstract mathematical concepts; they are essential tools used daily in various contexts:
1. Cooking and Baking:
Recipes often involve fractions. For instance, a recipe might call for 1/2 cup of sugar, 2/3 cup of flour, or 1/4 teaspoon of salt. Understanding fractions is crucial for precise measurements and successful cooking.
2. Measurements and Construction:
Construction and engineering projects rely heavily on accurate measurements. Fractions are used to represent precise dimensions, lengths, and quantities of materials. A carpenter might cut a piece of wood to 3 1/2 inches or a plumber might measure pipe lengths in fractions of feet.
3. Finance and Budgeting:
Fractions are integral to personal finance. Calculating discounts (e.g., 1/3 off), understanding interest rates (e.g., 5/100 or 0.05), and allocating a portion of your income (e.g., 1/4 for savings) all involve working with fractions.
4. Time Management:
Time is often measured and divided using fractions. For instance, a meeting might last 1/2 an hour, or a project deadline might be set for 3/4 of a year. Effectively managing time involves understanding and working with fractions.
5. Data Analysis and Statistics:
Fractions are fundamental in statistics and data analysis. Representing proportions, probabilities, and distributions often uses fractions or their decimal equivalents. Understanding data requires interpreting fractional representations.
Expanding the Concept: Working with More Complex Fractions
While the example of 1/7 of 42 is relatively simple, the principles extend to more complex scenarios:
Dealing with Improper Fractions:
If the problem involved a larger numerator, resulting in an improper fraction, we would convert it into a mixed number. For example, if we were calculating 5/7 of 42, we would get:
(5/7) * 42 = 210/7 = 30
Solving Problems with Multiple Fractions:
Calculations involving multiple fractions require understanding order of operations (PEMDAS/BODMAS). For example, finding 2/3 of 1/2 of 42 would involve multiplying the fractions first:
(2/3) * (1/2) * 42 = (2/6) * 42 = (1/3) * 42 = 14
Working with Decimals:
Fractions can be easily converted to decimals and vice-versa. This provides flexibility in solving problems, allowing you to use the most convenient format depending on the context. For example, 1/7 is approximately 0.143.
Conclusion: Mastering Fractions for a Broader Understanding
The seemingly simple question of "What is 1/7 of 42?" leads us to a deeper understanding of fractions, their significance, and their widespread applications. By mastering the principles of fraction calculation and recognizing their use in diverse fields, we enhance our mathematical literacy and equip ourselves with essential tools for navigating various aspects of life. From cooking to finance, construction to data analysis, fractions are an indispensable part of our numerical world. Therefore, a firm grasp of these foundational concepts is crucial for academic success and practical problem-solving. Continue practicing with different fraction problems, and you'll soon build the confidence and skills needed to tackle more complex calculations. Remember, the journey to mathematical proficiency is built one step—or rather, one fraction—at a time.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 7 Of 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.