What Expression Is Equivalent To 5z 2 3z 2 2
Greels
Apr 23, 2025 · 5 min read
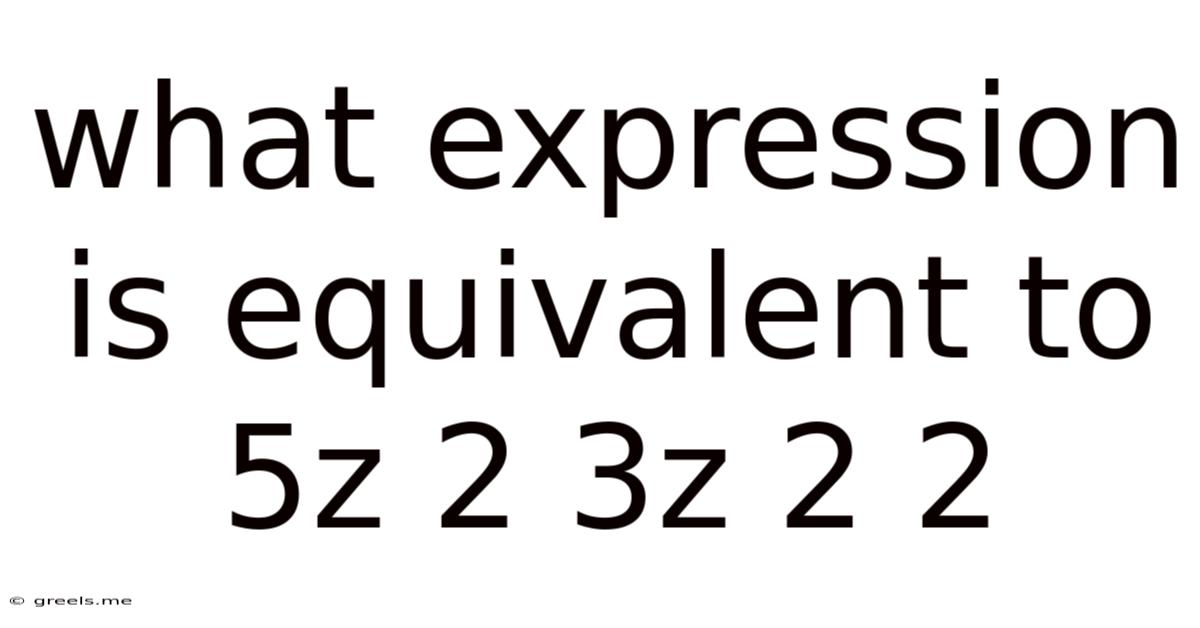
Table of Contents
What Expression is Equivalent to 5z² + 3z² + 2? Simplifying Algebraic Expressions
This article will delve into simplifying algebraic expressions, focusing specifically on finding an equivalent expression for 5z² + 3z² + 2. We'll explore the fundamental concepts of combining like terms, the order of operations (PEMDAS/BODMAS), and how to effectively simplify more complex algebraic expressions. Understanding these principles is crucial for success in algebra and beyond.
Understanding Like Terms
Before we tackle the simplification of 5z² + 3z² + 2, let's clarify the concept of "like terms." Like terms are terms in an algebraic expression that have the same variable(s) raised to the same power(s). In our expression, we have:
- 5z²: This term contains the variable 'z' raised to the power of 2. The coefficient (the number multiplying the variable) is 5.
- 3z²: This term also contains the variable 'z' raised to the power of 2. The coefficient is 3.
- 2: This is a constant term; it doesn't contain any variables.
Notice that 5z² and 3z² are like terms because they both have 'z²'. The constant term, 2, is not like either of the other terms.
Combining Like Terms: The Fundamental Principle
The key to simplifying algebraic expressions is to combine like terms. This involves adding or subtracting the coefficients of the like terms while keeping the variable and its exponent unchanged.
In our expression, 5z² + 3z² + 2, we can combine the like terms 5z² and 3z²:
5z² + 3z² = (5 + 3)z² = 8z²
Therefore, the simplified expression becomes:
8z² + 2
This is the equivalent expression to 5z² + 3z² + 2. We have successfully simplified the expression by combining the like terms.
The Order of Operations (PEMDAS/BODMAS)
While this particular expression is straightforward, it's crucial to understand the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This order dictates the sequence in which operations should be performed in any algebraic expression. Although not directly applicable to this simple example, understanding PEMDAS/BODMAS is vital when dealing with more complex expressions involving parentheses, exponents, and multiple operations.
Let's consider a slightly more complex scenario to illustrate the importance of PEMDAS/BODMAS:
3(2z² + 4) - 5z² + 10
- Parentheses/Brackets: First, we handle the expression within the parentheses: 2z² + 4. This cannot be simplified further.
- Multiplication: Next, we perform the multiplication: 3(2z² + 4) = 6z² + 12.
- Combine Like Terms: Now we have: 6z² + 12 - 5z² + 10. We combine the like terms 6z² and -5z² to get z². We also combine the constant terms 12 and 10 to get 22.
- Final Result: The simplified expression is z² + 22.
This example clearly demonstrates how crucial the order of operations is in simplifying more complex algebraic expressions.
More Complex Examples and Applications
Let's explore several more complex examples to further solidify our understanding of simplifying algebraic expressions:
Example 1:
4x³ + 2x² - 7x³ + 5x² + 3x - 1
Like terms: 4x³ and -7x³; 2x² and 5x².
Simplified Expression: -3x³ + 7x² + 3x - 1
Example 2:
(2y + 3)(y - 5)
This requires expanding the expression using the distributive property (also known as FOIL):
(2y + 3)(y - 5) = 2y(y) + 2y(-5) + 3(y) + 3(-5) = 2y² - 10y + 3y - 15
Simplified Expression: 2y² - 7y - 15
Example 3:
5a²b + 3ab² - 2a²b + 4ab²
Like terms: 5a²b and -2a²b; 3ab² and 4ab².
Simplified Expression: 3a²b + 7ab²
These examples highlight that the process of combining like terms remains consistent regardless of the complexity of the expression. The core principle remains the same: add or subtract the coefficients of like terms while keeping the variables and their exponents unchanged.
Applications of Simplifying Algebraic Expressions
Simplifying algebraic expressions is a fundamental skill in various areas of mathematics and science. Some key applications include:
- Solving Equations: Simplifying expressions is often a crucial first step in solving algebraic equations.
- Calculus: Simplifying expressions is essential for differentiating and integrating functions.
- Physics and Engineering: Simplifying expressions helps to model and solve problems in physics and engineering.
- Data Analysis: Simplifying expressions can help to analyze data more effectively.
- Computer Programming: Simplifying expressions can lead to more efficient and readable code.
Troubleshooting Common Mistakes
While simplifying algebraic expressions is a relatively straightforward process, several common mistakes can arise:
- Incorrectly Identifying Like Terms: Ensure that you accurately identify terms with the same variables raised to the same powers. Mistakes often occur when dealing with expressions containing multiple variables and exponents.
- Errors in Arithmetic: Pay close attention to the arithmetic operations involved in adding and subtracting coefficients. Double-check your calculations to minimize errors.
- Ignoring the Order of Operations: Always adhere to the order of operations (PEMDAS/BODMAS) to avoid incorrect simplification.
- Misunderstanding Negative Signs: Be cautious when dealing with negative signs. Make sure you correctly handle the signs when adding or subtracting terms.
Advanced Techniques and Further Learning
As you progress in your algebraic studies, you will encounter more sophisticated techniques for simplifying expressions, such as factoring, expanding binomials, and working with polynomials of higher degrees. These advanced techniques build upon the fundamental principles discussed in this article. Exploring resources like online tutorials, textbooks, and practice problems will enhance your understanding and proficiency in simplifying complex algebraic expressions.
Conclusion: Mastering the Fundamentals
Simplifying algebraic expressions is a fundamental skill that forms the cornerstone of many mathematical concepts. By understanding the principles of combining like terms and adhering to the order of operations, you can confidently simplify even the most complex expressions. Consistent practice and attention to detail are crucial for mastering this skill and achieving success in algebra and related fields. Remember, the equivalent expression for 5z² + 3z² + 2 is 8z² + 2. This foundational understanding sets you up for tackling more intricate algebraic challenges with ease and precision.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Expression Is Equivalent To 5z 2 3z 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.