Volume Of Solid Rotated About Y-axis Calculator
Greels
Mar 25, 2025 · 6 min read
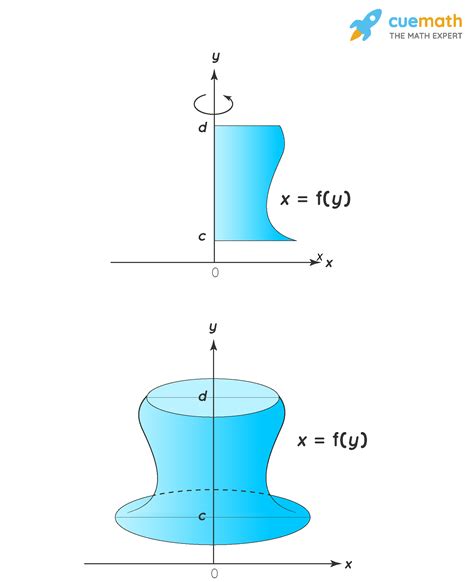
Table of Contents
Volume of Solid Rotated About Y-Axis Calculator: A Comprehensive Guide
Calculating the volume of a solid of revolution rotated around the y-axis can be a complex mathematical undertaking. However, understanding the underlying principles and utilizing the right tools can simplify the process significantly. This comprehensive guide explores the concept, different methods of calculation, potential challenges, and the practical application of a "volume of solid rotated about y-axis calculator."
Understanding Solids of Revolution
A solid of revolution is a three-dimensional figure formed by rotating a two-dimensional curve around an axis. Imagine taking a function graphed on the x-y plane and spinning it around the y-axis; the resulting 3D shape is a solid of revolution. The volume of this solid can be calculated using integral calculus. This process involves integrating infinitesimally thin cylindrical shells or disks along the axis of rotation.
The Importance of the Y-Axis
While the principles remain similar for rotation around the x-axis, rotating around the y-axis introduces a slight shift in how we set up the integral. The key difference lies in the expression for the radius and the limits of integration. When rotating about the y-axis, we integrate with respect to y, requiring us to express our function explicitly in terms of y (x = f(y)).
Methods for Calculating Volume: Shell and Disk Methods
There are two primary methods to calculate the volume of a solid of revolution around the y-axis: the shell method and the disk/washer method. The best approach depends on the complexity of the function and the shape of the solid.
1. The Shell Method
The shell method considers the volume as a sum of infinitely thin cylindrical shells. Each shell has a height determined by the function's value at a given y-coordinate, and its radius is simply the y-coordinate itself. The volume of a single shell is approximately 2π * y * f(y) * Δy, where Δy represents the thickness of the shell. To find the total volume, we integrate this expression over the appropriate range of y-values:
Formula: V = ∫<sub>a</sub><sup>b</sup> 2πy * f(y) dy
Where:
- V is the volume of the solid.
- a and b are the lower and upper limits of integration along the y-axis.
- y represents the radius of a cylindrical shell.
- f(y) represents the height of a cylindrical shell (the function expressed in terms of y).
- dy represents the thickness of a cylindrical shell.
When to use the Shell Method: The shell method is particularly useful when the function is easily expressed in terms of y and the resulting integral is relatively straightforward to solve. It's especially advantageous when the region is bounded by two curves.
2. The Disk/Washer Method
The disk/washer method considers the volume as a stack of infinitely thin disks or washers. For a solid generated by revolving a curve about the y-axis, each disk has a radius determined by the function's value at a given y-coordinate, and the thickness is dy. If the solid is formed from a region bounded by two curves, f(y) and g(y), then we use washers instead of disks. The volume of a single washer is approximately π * [f(y)² - g(y)²] * Δy. Integrating this expression over the appropriate y-range gives the total volume:
Formula (Disk): V = ∫<sub>a</sub><sup>b</sup> π[f(y)]² dy (for a region bounded by the y-axis and a single curve)
Formula (Washer): V = ∫<sub>a</sub><sup>b</sup> π[f(y)² - g(y)²] dy (for a region bounded by two curves)
Where:
- V is the volume of the solid.
- a and b are the lower and upper limits of integration along the y-axis.
- f(y) represents the outer radius of a washer.
- g(y) represents the inner radius of a washer.
- dy represents the thickness of a disk or washer.
When to use the Disk/Washer Method: The disk/washer method is preferable when the function is easily expressed in terms of y, and the region is relatively simple. It's often more straightforward than the shell method for regions bounded by the y-axis and a single curve.
Challenges in Calculation
While conceptually straightforward, the practical application of these methods can present several challenges:
-
Expressing the Function in Terms of y: This is often the most difficult step. It requires solving the original equation for x in terms of y, which may not always be possible or easy.
-
Determining the Limits of Integration: Accurately identifying the y-coordinates that define the region being rotated is crucial. Incorrect limits will lead to an incorrect volume calculation.
-
Solving the Integral: Evaluating the resulting integral can be computationally intensive, especially for complex functions. Sometimes numerical integration techniques are necessary.
-
Choosing the Appropriate Method: Deciding whether to use the shell or disk/washer method often involves assessing the complexity of the resulting integrals. Sometimes one method is significantly easier than the other.
The Role of a Volume of Solid Rotated About Y-Axis Calculator
A dedicated "volume of solid rotated about y-axis calculator" can significantly simplify the process. These online tools typically require the user to input the function, the limits of integration, and the method (shell or disk/washer). The calculator then performs the integration and provides the calculated volume.
Benefits of Using a Calculator
-
Reduced Computational Effort: The calculator handles the complex integration process, freeing the user from tedious manual calculations.
-
Increased Accuracy: Calculators minimize the risk of human error in integration.
-
Time Savings: The calculation process is significantly faster than manual computation, especially for complex functions.
-
Accessibility: Calculators make volume calculations accessible to individuals without advanced mathematical expertise.
Limitations of Using a Calculator
-
Understanding the Underlying Principles: Relying solely on calculators without understanding the underlying concepts of integration and solids of revolution can hinder learning and problem-solving abilities.
-
Input Errors: Incorrectly entering the function or limits of integration will lead to erroneous results.
-
Limited Functionality: Some calculators may not handle all types of functions or integration methods.
-
Over-reliance: Excessive reliance on calculators can hinder the development of problem-solving skills.
Practical Applications
Calculating the volume of solids of revolution around the y-axis has wide-ranging applications in various fields:
-
Engineering: Designing pipes, tanks, and other cylindrical structures.
-
Physics: Calculating the volume of irregularly shaped objects.
-
Architecture: Determining the volume of curved structures.
-
Computer Graphics: Generating 3D models using rotational symmetry.
-
Manufacturing: Calculating the amount of material needed to produce parts with rotational symmetry.
Conclusion
Calculating the volume of a solid of revolution around the y-axis involves understanding the principles of integration and selecting the appropriate method (shell or disk/washer). While manual calculation can be challenging, a "volume of solid rotated about y-axis calculator" offers a powerful tool for efficient and accurate computation. However, it's essential to retain an understanding of the underlying mathematical concepts to use the calculator effectively and interpret the results meaningfully. Combining the power of computational tools with a strong grasp of fundamental principles ensures success in tackling these complex mathematical problems. Remember to always double-check your input values and understand the limitations of any calculator you use. The most effective approach often involves a combination of manual analysis and computational assistance to ensure accurate and efficient results.
Latest Posts
Latest Posts
-
How Many Kg Is 205 Pounds
Mar 28, 2025
-
91 Kg Is How Many Pounds
Mar 28, 2025
-
120 Km Is How Many Miles
Mar 28, 2025
-
How Many Miles In 250 Kilometers
Mar 28, 2025
-
How Many Kilograms In 175 Pounds
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Volume Of Solid Rotated About Y-axis Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
