Vertex And Axis Of Symmetry Calculator
Greels
Mar 30, 2025 · 6 min read
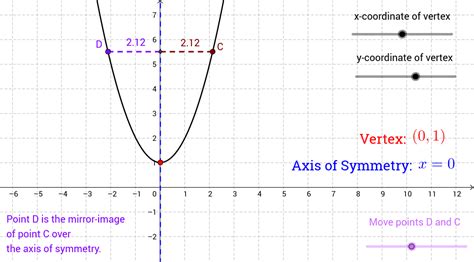
Table of Contents
Vertex and Axis of Symmetry Calculator: A Comprehensive Guide
Finding the vertex and axis of symmetry of a parabola can be a crucial step in various mathematical applications, from graphing quadratic functions to solving optimization problems. While manual calculations are possible, using a vertex and axis of symmetry calculator can significantly streamline the process, saving time and reducing the risk of errors. This comprehensive guide explores the concepts of vertex and axis of symmetry, their significance, and how to effectively use a calculator to determine these key features of a parabola. We'll also delve into various types of quadratic equations and how to adapt the calculator's input for optimal results.
Understanding Parabolas, Vertices, and Axes of Symmetry
A parabola is a U-shaped curve representing a quadratic function, typically expressed in the form:
f(x) = ax² + bx + c
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The shape and orientation of the parabola are determined by the value of 'a'. If 'a' is positive, the parabola opens upwards; if 'a' is negative, it opens downwards.
The vertex is the highest or lowest point on the parabola, depending on whether it opens downwards or upwards, respectively. It represents the minimum or maximum value of the quadratic function. The vertex plays a critical role in understanding the behavior of the quadratic function, especially in real-world applications like projectile motion or optimization problems.
The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetrical halves. It's a line of reflection: for any point on one side of the axis, there's a corresponding point on the other side equidistant from the axis. The equation of the axis of symmetry is a simple vertical line, always of the form x = h, where (h, k) represents the coordinates of the vertex.
Manual Calculation vs. Calculator Usage
While the vertex and axis of symmetry can be calculated manually using formulas derived from the quadratic equation's standard form, the process can be prone to errors, especially with more complex equations. The formulas are:
- x-coordinate of the vertex (h): h = -b / 2a
- y-coordinate of the vertex (k): k = f(h) (Substitute the value of 'h' back into the original quadratic equation)
- Axis of symmetry: x = h
These formulas are straightforward for simple equations but can become cumbersome with larger coefficients or fractional values. A vertex and axis of symmetry calculator offers a more efficient and accurate alternative.
How to Use a Vertex and Axis of Symmetry Calculator
Most online calculators require you to input the coefficients 'a', 'b', and 'c' from your quadratic equation. The interface is usually straightforward and intuitive:
-
Identify the coefficients: Write your quadratic equation in the standard form (ax² + bx + c). Clearly identify the values of 'a', 'b', and 'c'. Be mindful of the signs – a negative coefficient should be entered with a negative sign.
-
Input the coefficients: Enter the values of 'a', 'b', and 'c' into the corresponding fields of the calculator. Double-check your input to avoid errors.
-
Calculate: Click the "Calculate" or equivalent button.
-
Interpret the results: The calculator will typically output the x-coordinate and y-coordinate of the vertex, and the equation of the axis of symmetry. For example, the output might be: Vertex: (2, -1), Axis of Symmetry: x = 2.
Different Forms of Quadratic Equations
While the standard form (ax² + bx + c) is common, quadratic equations can also be presented in other forms:
-
Vertex Form: f(x) = a(x - h)² + k. In this form, the vertex (h, k) is directly visible. A calculator might accept input in this form, although it’s usually better to convert to standard form for consistency.
-
Factored Form: f(x) = a(x - r₁)(x - r₂). This form shows the x-intercepts (roots) of the quadratic equation, r₁ and r₂. While not directly providing the vertex and axis of symmetry, it can be helpful for understanding the parabola's behavior. Conversion to standard form is recommended before using the calculator.
-
Intercept Form: Similar to the factored form, this explicitly presents the x-intercepts.
Advanced Applications and Considerations
The vertex and axis of symmetry are not just abstract mathematical concepts; they have significant applications in various fields:
-
Projectile Motion: In physics, the trajectory of a projectile is often modeled using a quadratic equation. The vertex represents the highest point reached by the projectile, and the axis of symmetry indicates the point at which the projectile reaches its maximum height.
-
Optimization Problems: In business and engineering, optimization problems often involve finding the maximum or minimum value of a function. The vertex of a parabola representing a quadratic cost or profit function provides the optimal solution.
-
Graphing Quadratic Functions: Knowing the vertex and axis of symmetry is essential for accurately sketching the graph of a quadratic function. The vertex gives a central point, and the symmetry allows efficient plotting of additional points.
-
Solving Quadratic Inequalities: The vertex and axis of symmetry are helpful in visualizing and solving quadratic inequalities. The parabola's position relative to the x-axis is key to determining solution sets.
Choosing and Using the Right Calculator
Numerous online vertex and axis of symmetry calculators are available. When selecting one, consider factors like:
-
Interface: Look for a calculator with a clean, user-friendly interface. Easy input and clear output are essential.
-
Accuracy: Ensure the calculator provides accurate results, especially for complex equations. You can test this with known equations and compare results to manual calculations.
-
Additional Features: Some calculators may offer additional features like graphing capabilities or step-by-step solutions.
Troubleshooting and Common Mistakes
-
Incorrect Input: The most common mistake is entering incorrect coefficients. Always double-check your input before calculating.
-
Units: Make sure your input values are consistent. If dealing with real-world problems, ensure consistent units of measurement.
-
Understanding the Output: Ensure you understand what the calculator is providing. The output should clearly state the vertex coordinates (x,y) and the equation of the axis of symmetry.
-
Choosing the Appropriate Form: Using the wrong form of the quadratic equation can lead to errors. Always convert to standard form if needed for optimal use.
Conclusion
A vertex and axis of symmetry calculator is an invaluable tool for quickly and accurately determining the key features of a parabola. While manual calculation offers valuable understanding, using a calculator saves time and reduces errors, especially when dealing with complex equations or numerous calculations. By understanding the concepts of parabolas, vertices, and axes of symmetry, and by using a reliable calculator effectively, you can greatly enhance your ability to solve quadratic equations and apply these concepts to real-world problems. Remember to always check your input and ensure you are using the correct form of the equation to obtain accurate and reliable results. Mastering these techniques enhances your mathematical proficiency and allows you to confidently tackle challenging problems in various fields.
Latest Posts
Latest Posts
-
2 N 3 7 5 2n
Apr 01, 2025
-
131 Kg Is How Many Pounds
Apr 01, 2025
-
Integrate X 3 X 2 1
Apr 01, 2025
-
Cuanto Es 208 Libras En Kilos
Apr 01, 2025
-
130 Miles Per Hour In Kilometers
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Vertex And Axis Of Symmetry Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
