The Sum Of Twice A Number And 10 Is 36
Greels
Apr 23, 2025 · 5 min read
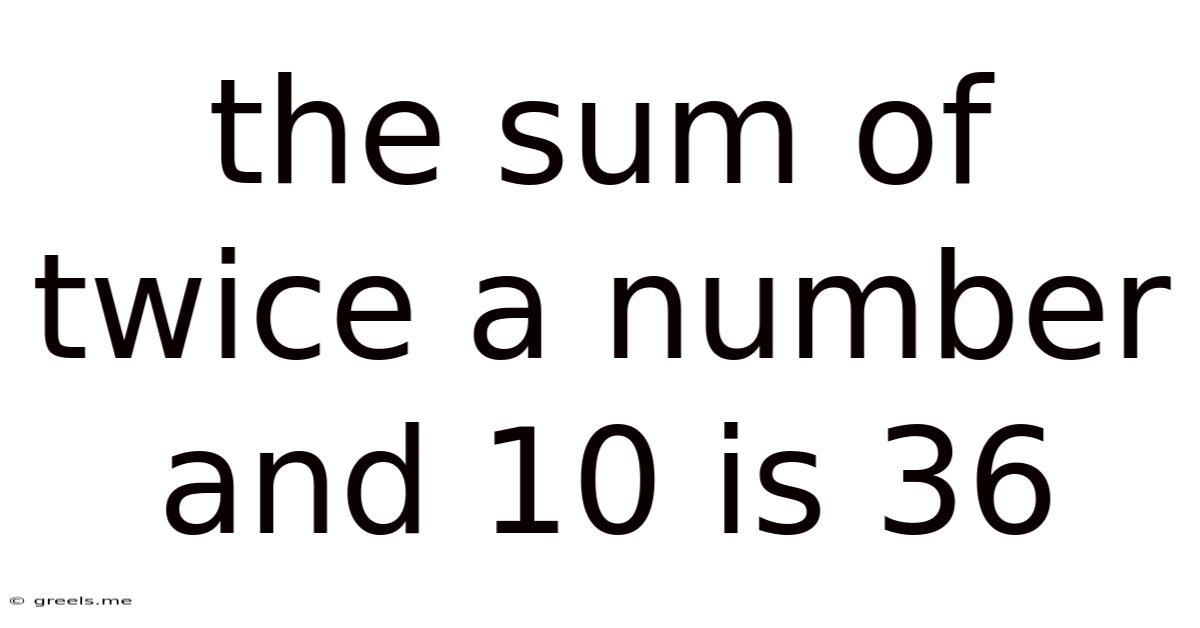
Table of Contents
The Sum of Twice a Number and 10 is 36: A Deep Dive into Problem Solving and Mathematical Concepts
This seemingly simple mathematical statement, "The sum of twice a number and 10 is 36," opens a door to a world of problem-solving techniques, algebraic manipulations, and fundamental mathematical concepts. While the solution might appear straightforward at first glance, exploring this problem allows us to delve deeper into the underlying principles and broaden our understanding of mathematics.
Understanding the Problem: Deconstructing the Statement
The problem presents a word problem, a common type of question in mathematics that requires translating words into mathematical expressions. Let's break down the statement piece by piece:
- "A number": This represents an unknown value, typically denoted by a variable, often 'x'.
- "Twice a number": This translates to multiplying the number (x) by 2, resulting in 2x.
- "The sum of twice a number and 10": This indicates the addition of 2x and 10, creating the expression 2x + 10.
- "is 36": This signifies that the expression 2x + 10 is equal to 36, leading to the equation 2x + 10 = 36.
Solving the Equation: Unveiling the Unknown
Now that we have formulated the equation, 2x + 10 = 36, we can employ algebraic techniques to solve for the unknown variable, 'x'. The goal is to isolate 'x' on one side of the equation. Here's a step-by-step approach:
-
Subtract 10 from both sides: This eliminates the constant term from the left side, maintaining the balance of the equation.
2x + 10 - 10 = 36 - 10 2x = 26 -
Divide both sides by 2: This isolates 'x', revealing its value.
2x / 2 = 26 / 2 x = 13
Therefore, the number is 13.
Verifying the Solution: Checking Our Work
It's crucial to verify our solution by substituting the value of 'x' back into the original equation:
2x + 10 = 36
2(13) + 10 = 36
26 + 10 = 36
36 = 36
The equation holds true, confirming that our solution, x = 13, is correct.
Expanding the Scope: Exploring Related Concepts
This simple problem serves as a gateway to exploring several interconnected mathematical concepts:
1. Variables and Equations: The Building Blocks of Algebra
The problem highlights the fundamental role of variables (like 'x') in representing unknown quantities and the importance of equations in establishing relationships between these quantities. Understanding how to manipulate equations is crucial for solving a wide range of mathematical problems.
2. Inverse Operations: Undoing Mathematical Actions
The solution process utilizes inverse operations – subtraction to undo addition, and division to undo multiplication. This concept is fundamental to solving equations and manipulating algebraic expressions.
3. Order of Operations (PEMDAS/BODMAS): Maintaining Mathematical Integrity
While not explicitly emphasized in this particular problem, the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is implicitly followed. Understanding this order is essential for correctly evaluating expressions and solving more complex equations.
4. Problem-Solving Strategies: A Systematic Approach
The process of translating a word problem into a mathematical equation and then solving it demonstrates a systematic approach to problem-solving. This approach is applicable to many fields beyond mathematics.
5. Real-World Applications: Mathematics in Everyday Life
Although seemingly abstract, this type of problem finds applications in numerous real-world scenarios. For instance, it could be used to model situations involving costs, quantities, or distances. Understanding such basic equations allows us to approach real-world situations with a more analytical and quantitative lens.
Beyond the Basics: Extending the Problem
We can extend this problem in various ways to deepen our understanding and explore more complex scenarios:
1. Introducing Inequalities: Exploring Ranges of Solutions
Instead of an equation (2x + 10 = 36), we could create an inequality (e.g., 2x + 10 > 36 or 2x + 10 < 36). This would lead to a range of possible solutions for 'x', introducing the concept of inequalities and their graphical representation.
2. Adding More Variables: Exploring Systems of Equations
We could introduce another variable and another equation, creating a system of equations. Solving such a system requires more sophisticated techniques, such as substitution or elimination.
3. Introducing Functions: Generalizing the Relationship
We can generalize the relationship between the number and its result as a function: f(x) = 2x + 10. This allows us to explore the properties of this function, such as its domain, range, and graph.
4. Exploring Different Number Systems: Expanding the Scope
We could explore the solution to the equation in different number systems, such as complex numbers. This would introduce new mathematical concepts and techniques.
5. Word Problem Variations: Developing Problem-Solving Skills
Creating similar word problems with different contexts helps in developing strong problem-solving skills. This reinforces the ability to translate word problems into mathematical equations. Examples could involve:
- "The sum of three times a number and 5 is 20."
- "If you double a number and add 7, the result is 19. Find the number."
- "A rectangle has a length that is twice its width. If the perimeter is 30, find the dimensions."
Conclusion: The Power of Simple Equations
The seemingly trivial problem "The sum of twice a number and 10 is 36" provides a robust foundation for understanding fundamental mathematical concepts, problem-solving techniques, and their applications. By exploring this problem and its extensions, we can gain a deeper appreciation of the power and versatility of simple equations and their role in unlocking the secrets of the mathematical world. The process of solving such equations is not just about finding the answer; it's about understanding the underlying logic, building problem-solving skills, and developing a deeper appreciation for the beauty and elegance of mathematics. This simple equation is a stepping stone to more advanced mathematical concepts, highlighting the interconnectedness of mathematical ideas and their relevance to our world. The journey from a simple word problem to a broader understanding of mathematical principles is a testament to the power and beauty of mathematical exploration.
Latest Posts
Related Post
Thank you for visiting our website which covers about The Sum Of Twice A Number And 10 Is 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.