The Sum Of 5 Consecutive Integers Is 265.
Greels
Apr 14, 2025 · 5 min read
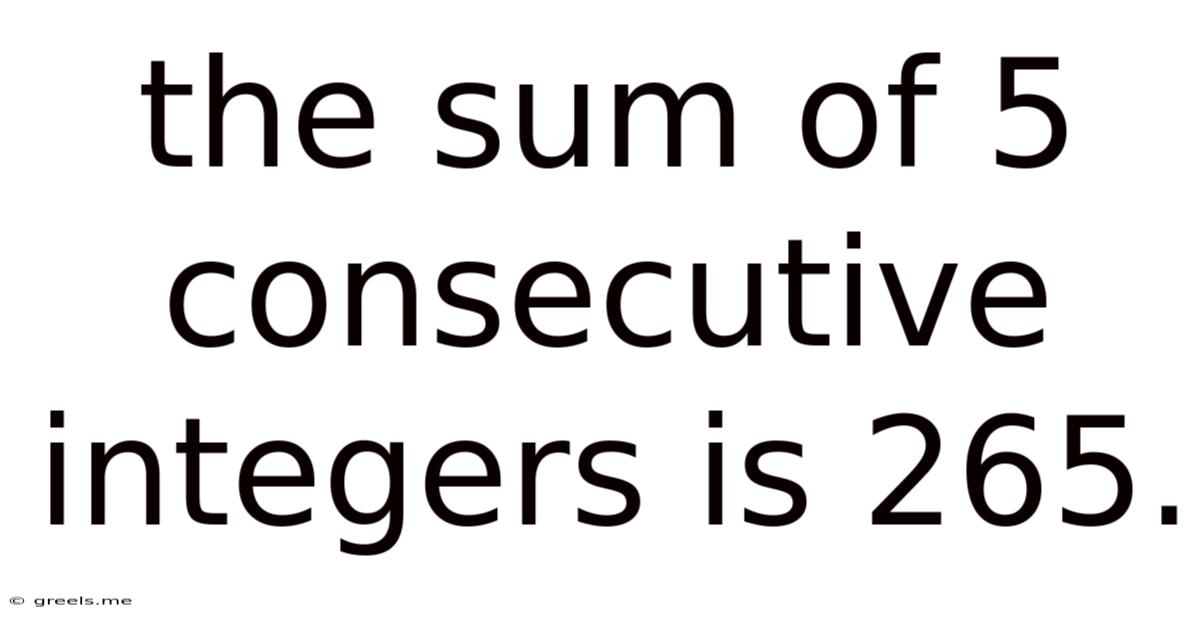
Table of Contents
The Sum of 5 Consecutive Integers is 265: Unraveling the Math and Exploring Extensions
The seemingly simple statement, "The sum of 5 consecutive integers is 265," opens a door to a fascinating exploration of mathematical principles, problem-solving strategies, and their broader applications. This seemingly basic arithmetic problem provides a springboard for understanding more complex concepts, from algebraic manipulation to the power of mathematical induction. Let's delve into this problem and uncover its hidden depths.
Understanding the Problem
At its core, the problem presents a straightforward equation: finding five consecutive integers (numbers following each other directly, like 1, 2, 3, 4, 5) whose sum equals 265. This can be approached using several methods, each offering valuable insights into different mathematical techniques.
Method 1: Algebraic Approach
Let's represent the five consecutive integers algebraically. We can denote the smallest integer as 'x'. The next four consecutive integers would then be x+1, x+2, x+3, and x+4. The sum of these integers is given as 265. This allows us to formulate the equation:
x + (x+1) + (x+2) + (x+3) + (x+4) = 265
Simplifying the equation, we get:
5x + 10 = 265
Subtracting 10 from both sides:
5x = 255
Dividing both sides by 5:
x = 51
Therefore, the five consecutive integers are 51, 52, 53, 54, and 55. We can verify this by adding them together: 51 + 52 + 53 + 54 + 55 = 265. This confirms our solution.
Method 2: Average Approach
Another elegant approach utilizes the concept of averages. Since we are dealing with consecutive integers, the average of these five numbers will be the middle number. The sum of the five integers is 265, so their average is 265/5 = 53. Because the numbers are consecutive, the middle number must be 53. Therefore, the five integers are 51, 52, 53, 54, and 55. This method highlights the power of using averages to simplify problems involving consecutive numbers.
Extending the Problem: Exploring Variations and Generalizations
The initial problem provides a foundation for exploring a wider range of similar problems. Let's consider some extensions:
1. Sum of n Consecutive Integers
Instead of five consecutive integers, what if we were asked to find the sum of n consecutive integers? We can generalize the algebraic approach. Let the first integer be 'x'. The sum of n consecutive integers can be represented as:
x + (x+1) + (x+2) + ... + (x+n-1) = S (where S is the given sum)
This simplifies to:
nx + (1+2+...+n-1) = S
Using the formula for the sum of an arithmetic series, 1+2+...+(n-1) = (n-1)n/2, the equation becomes:
nx + (n-1)n/2 = S
This equation can be solved for x, allowing us to find the first integer in the sequence for any given sum (S) and number of consecutive integers (n). For instance, if we wanted to find 7 consecutive integers that sum to 525, we could use this generalized formula.
2. Finding Consecutive Even or Odd Integers
The problem can be adapted to finding consecutive even or odd integers. For example, "The sum of 5 consecutive even integers is 270." The approach remains similar, but we need to modify the algebraic representation. Let's represent the first even integer as 2x. The consecutive even integers would be 2x, 2x+2, 2x+4, 2x+6, and 2x+8. The equation becomes:
2x + (2x+2) + (2x+4) + (2x+6) + (2x+8) = 270
Solving this equation would give us the first even integer, and subsequently, the entire sequence. A similar approach can be applied for consecutive odd integers.
3. Word Problems and Real-World Applications
This type of problem isn't limited to abstract mathematical exercises. It can be embedded within word problems that reflect real-world situations. For example, consider a scenario involving seating arrangements at a conference, ticket sales at a theatre, or the distribution of resources. These applications highlight the practical utility of understanding the principles of consecutive integer sums.
Deeper Mathematical Concepts: Connecting to Advanced Ideas
The seemingly simple problem touches upon more advanced mathematical ideas:
1. Arithmetic Progressions
The sequence of consecutive integers forms an arithmetic progression – a sequence where the difference between consecutive terms is constant (in this case, 1). Understanding arithmetic progressions is crucial in various mathematical fields, including calculus and number theory.
2. Mathematical Induction
Mathematical induction is a powerful technique for proving statements about all positive integers. It can be used to formally prove the general formula derived for the sum of n consecutive integers. The process involves proving a base case (e.g., for n=1) and then showing that if the statement holds for n=k, it also holds for n=k+1. This proves the statement holds for all positive integers.
3. Number Theory
The problem touches upon number theory, a branch of mathematics focused on the properties of integers. Exploring variations of this problem can lead to deeper investigations into divisibility, prime numbers, and other fascinating number-theoretic concepts.
Conclusion: From Simple Problem to Broad Understanding
The problem of summing five consecutive integers to 265, while seemingly elementary, serves as a powerful introduction to various mathematical concepts and problem-solving techniques. By exploring its variations and extensions, we uncover its deeper connections to algebra, arithmetic progressions, mathematical induction, and number theory. This seemingly simple problem provides a valuable lesson in the interconnectedness of mathematical ideas and their applications in diverse contexts. This process of exploration encourages critical thinking, analytical skills, and a deeper appreciation for the beauty and power of mathematics. The ability to approach a problem from multiple angles, as demonstrated here through algebraic and average approaches, is a crucial skill in both mathematics and problem-solving in general. This extends beyond the realm of pure mathematics, finding applications in fields like computer science, engineering, and finance. The principles explored here are fundamental building blocks for more complex mathematical endeavors. Therefore, mastering the understanding of consecutive integer sums and their generalizations is a valuable asset for anyone interested in pursuing a deeper understanding of mathematics and its applications in various fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about The Sum Of 5 Consecutive Integers Is 265. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.