The Difference Of A Number And 5
Greels
May 02, 2025 · 5 min read
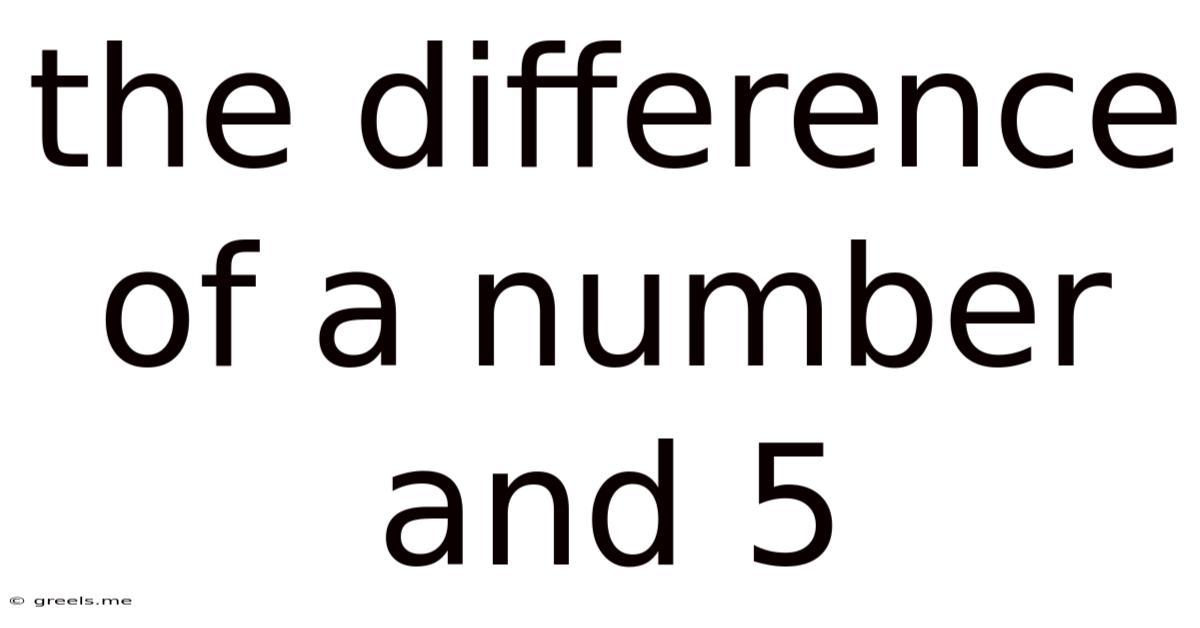
Table of Contents
The Fascinating World of Numbers: Exploring the Difference Between a Number and 5
The seemingly simple concept of finding the difference between a number and 5 opens a door to a vast and fascinating world of mathematical exploration. While the basic arithmetic is straightforward, delving deeper reveals intricate connections to various mathematical concepts, problem-solving techniques, and even real-world applications. This article aims to provide a comprehensive exploration of this seemingly simple concept, revealing its complexities and highlighting its significance in diverse mathematical contexts.
Understanding the Fundamentals: Subtraction and the Concept of Difference
At its core, finding the difference between a number and 5 involves subtraction. Subtraction is one of the four fundamental arithmetic operations, representing the process of removing a quantity from another. In the context of "the difference between a number and 5," we're essentially asking: what remains when 5 is subtracted from a given number?
The formula is simple: Number - 5 = Difference
For instance:
- If the number is 10, the difference is 10 - 5 = 5
- If the number is 2, the difference is 2 - 5 = -3 (note the negative result)
- If the number is 5, the difference is 5 - 5 = 0
This simple operation lays the groundwork for understanding more complex scenarios.
Exploring Different Number Types: Integers, Decimals, and Beyond
The "number" in our equation can represent a variety of numerical types:
-
Integers: These are whole numbers, both positive and negative (e.g., -3, 0, 5, 10, 100). Calculating the difference between an integer and 5 is straightforward.
-
Decimals: These numbers include a fractional part (e.g., 3.14, 7.5, -2.8). Subtracting 5 from a decimal involves standard decimal subtraction, ensuring proper alignment of the decimal point.
-
Rational Numbers: These are numbers expressible as a fraction (e.g., 1/2, 3/4, -5/7). Finding the difference between a rational number and 5 involves converting the 5 into a fraction with a common denominator before performing the subtraction.
-
Irrational Numbers: These numbers cannot be expressed as a simple fraction (e.g., π, √2). Subtracting 5 from an irrational number results in another irrational number. Calculations often involve approximations.
-
Complex Numbers: These numbers contain both a real and an imaginary part (e.g., 3 + 2i). Subtracting 5 from a complex number involves subtracting 5 from the real part, leaving the imaginary part unchanged.
Beyond Basic Subtraction: Expanding the Concept
While the basic operation is simple, the concept of "the difference between a number and 5" can be extended in several ways, enriching its mathematical significance:
1. Absolute Difference: Focusing on Magnitude
The absolute difference ignores the sign, focusing solely on the magnitude of the difference. It's represented by using absolute value notation: |Number - 5|.
For example:
- If the number is 10, the absolute difference is |10 - 5| = 5
- If the number is 2, the absolute difference is |2 - 5| = |-3| = 3
The absolute difference is particularly useful in situations where the direction of the difference isn't crucial, such as measuring error or discrepancy.
2. Inequalities and the Concept of Range
The difference between a number and 5 can be used to define inequalities. For example:
-
|Number - 5| < 2: This inequality represents all numbers whose difference from 5 is less than 2. This translates to a range of numbers between 3 and 7 (exclusive).
-
Number - 5 > 10: This inequality represents all numbers greater than 15.
Understanding inequalities adds a layer of sophistication to the concept, allowing for the definition of number ranges and the solution of mathematical problems involving constraints.
3. Functions and Mapping: A Functional Perspective
We can represent the operation of finding the difference between a number and 5 as a function:
f(x) = x - 5
Where 'x' represents the input number, and 'f(x)' represents the output (the difference). This functional representation allows for a more abstract and general understanding of the operation. We can analyze the function's properties, such as its domain (all real numbers) and its range (all real numbers).
4. Applications in Problem Solving
The concept of "the difference between a number and 5" appears frequently in various problem-solving scenarios. Consider these examples:
-
Age Problems: "John is 5 years older than Mary. If John is x years old, how old is Mary?" The solution involves finding the difference between John's age (x) and 5 (x - 5).
-
Temperature Differences: "The temperature dropped by 5 degrees. If the current temperature is x degrees, what was the temperature before the drop?" Again, we need to find the difference (x + 5).
-
Measurement Discrepancies: "A measurement is expected to be 5 units. If the actual measurement is x units, what's the discrepancy?" This involves finding the difference |x - 5|.
These examples demonstrate the practical applicability of this seemingly simple mathematical concept across various fields.
Advanced Concepts and Extensions
The exploration of "the difference between a number and 5" can be extended to more advanced mathematical concepts:
1. Calculus and Limits
In calculus, the concept of a limit can be applied to explore the behavior of the difference as the number approaches a specific value. For example, we could analyze the limit of the function f(x) = x - 5 as x approaches infinity or a specific number.
2. Abstract Algebra
In abstract algebra, the concept of a difference can be generalized to other algebraic structures, beyond the real numbers.
Conclusion: A Simple Concept with Profound Implications
While the initial impression of "the difference between a number and 5" might be one of simplicity, a deeper examination reveals its multifaceted nature. From basic arithmetic to advanced mathematical concepts, the idea permeates various branches of mathematics and finds practical application in problem-solving across diverse fields. Understanding this seemingly simple concept thoroughly provides a strong foundation for further mathematical exploration and enhances problem-solving capabilities. The seemingly trivial calculation opens doors to a rich understanding of mathematical principles and their real-world relevance. Its seemingly simple nature belies its profound implications within the broader landscape of mathematics and its applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about The Difference Of A Number And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.