Square Root Of X 3 X 3
Greels
Apr 05, 2025 · 5 min read
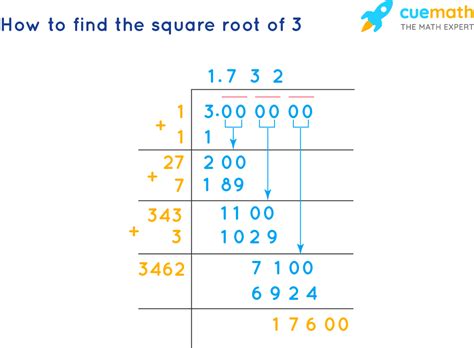
Table of Contents
Decoding the Enigma: A Deep Dive into the Square Root of x³ + 3x³
The expression "square root of x³ + 3x³" presents a seemingly simple mathematical challenge, yet it unlocks a pathway to understanding fundamental algebraic concepts and their practical applications. This article will dissect this expression, exploring its simplification, graphical representation, and broader implications within the realm of mathematics and beyond. We will delve into various approaches to solving this, considering different scenarios and levels of mathematical sophistication.
Understanding the Core Components
Before tackling the square root of x³ + 3x³, let's first solidify our understanding of the individual components:
1. Cubic Terms (x³):
The term 'x³' represents a cubic term, meaning a variable (x) raised to the power of 3. Geometrically, this can be visualized as the volume of a cube with sides of length x. Algebraically, it signifies the result of multiplying x by itself three times (x * x * x). Understanding cubic terms is crucial for manipulating and simplifying higher-order polynomial expressions.
2. The Summation (x³ + 3x³):
The expression x³ + 3x³ involves the addition of two like terms. This is a fundamental algebraic operation. Since both terms contain x raised to the power of 3, they can be combined directly. The process is analogous to adding apples and apples – you simply add the quantities.
3. The Square Root Operator (√):
The square root operator (√) represents the inverse operation of squaring a number. In other words, it finds a value that, when multiplied by itself, equals the number under the root. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. The square root of a variable expression, like our x³ + 3x³, follows the same principle.
Simplifying the Expression: A Step-by-Step Approach
Now, let's simplify the expression "square root of x³ + 3x³":
-
Combine Like Terms: The first step is to simplify the expression within the square root. As mentioned earlier, x³ + 3x³ simplifies to 4x³. This is achieved by adding the coefficients (1 + 3 = 4) while keeping the variable and exponent unchanged.
-
Applying the Square Root: Now, we have √(4x³). The square root can be applied to both the coefficient and the variable separately.
-
Simplifying the Coefficient: The square root of 4 is 2 (because 2 * 2 = 4).
-
Simplifying the Variable: The square root of x³ can be simplified using the properties of exponents. Recall that √x³ is equivalent to (x³)^(1/2). Using the power of a power rule in algebra, this simplifies to x^(3/2). This can also be expressed as x * √x.
-
Final Simplified Form: Combining these simplifications, the expression "square root of x³ + 3x³" simplifies to 2x√x or 2x^(3/2).
Graphical Representation and Interpretation
The simplified expression, 2x√x, can be represented graphically. Plotting this function reveals its behavior and characteristics. The graph will show a curve that starts at the origin (0,0) and increases steadily as x increases. The function is defined only for non-negative values of x because the square root of a negative number is not a real number. The curve's steepness increases as x grows, indicating that the function's growth rate accelerates.
Analyzing the graph provides insights into the relationship between x and the expression's value. For small values of x, the output is relatively small, while for larger x, the output increases significantly.
Extending the Concept: Real-World Applications
While seemingly abstract, the concept of simplifying square roots of polynomial expressions finds practical applications in various fields:
-
Physics: Calculations involving volumes, areas, and other geometrical quantities often involve square roots and higher-order terms. For instance, determining the radius of a sphere given its volume involves operations similar to simplifying our expression.
-
Engineering: Structural analysis, fluid dynamics, and many other engineering disciplines utilize mathematical models that involve complex expressions including square roots and higher-order polynomials.
-
Computer Graphics: The generation of smooth curves and surfaces in computer graphics often relies on mathematical functions, including those that involve square roots and higher-order terms like the one we’ve explored.
-
Finance: Complex financial models for calculating investment returns and assessing risk often use sophisticated mathematical functions. Square roots and polynomials are fundamental components in many of these models.
Addressing Potential Challenges and Variations
This exploration has focused on the simplification of the expression assuming positive values for 'x'. Let's examine some additional complexities:
-
Negative Values of x: If x were negative, we would need to consider the concept of complex numbers, as the square root of a negative number is not a real number. This would introduce the imaginary unit "i" (where i² = -1) into the solution.
-
More Complex Expressions: The principles we’ve illustrated here are foundational. Similar techniques can be applied to even more intricate expressions involving multiple variables and higher-order terms. Mastering these fundamentals paves the way for tackling such complexities.
-
Numerical Solutions: For expressions that defy simple algebraic simplification, numerical methods (such as iterative techniques) can provide approximate solutions. These methods are crucial in dealing with equations that lack analytical solutions.
Conclusion: A Foundation for Further Exploration
The seemingly simple expression, "square root of x³ + 3x³," opens a door to a broader understanding of algebraic manipulation, graphical representation, and real-world applications. By carefully dissecting each component, simplifying the expression, and exploring its graphical behavior, we’ve built a strong foundation. This exploration reinforces fundamental mathematical concepts and underscores the importance of algebraic skills in tackling complex problems across diverse disciplines. Furthermore, understanding the nuances of square roots and their interactions with polynomials empowers individuals to solve a wide range of mathematical challenges and appreciate the beauty and power of mathematical thinking. Remember to always approach these types of problems systematically, step-by-step, and to understand the underlying principles. This solid foundation will serve you well in future mathematical endeavors.
Latest Posts
Latest Posts
-
32 Kg Equals How Many Pounds
Apr 06, 2025
-
How Many Feet Are In 121 Inches
Apr 06, 2025
-
What Is 80 Centimeters In Inches
Apr 06, 2025
-
220 Mm Is How Many Inches
Apr 06, 2025
-
55 In Is How Many Feet
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
