Solve The System Of Equations Using Elimination Calculator
Greels
Mar 31, 2025 · 6 min read
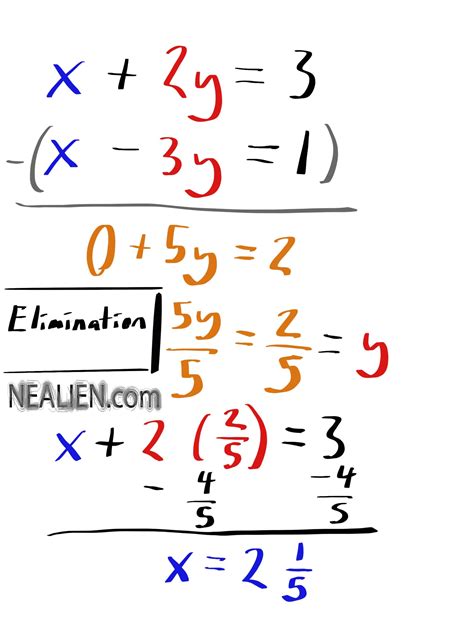
Table of Contents
Solve the System of Equations Using Elimination Calculator: A Comprehensive Guide
Solving systems of equations is a fundamental concept in algebra, appearing frequently in various fields like physics, engineering, economics, and computer science. While simple systems can be solved manually, more complex systems often require the assistance of tools like elimination calculators. This comprehensive guide explores the elimination method, its applications, and how to effectively use an elimination calculator to solve systems of equations. We'll delve into the underlying mathematics, address common challenges, and provide practical examples to solidify your understanding.
Understanding Systems of Equations and the Elimination Method
A system of equations is a set of two or more equations with the same variables. The goal is to find the values of the variables that satisfy all equations simultaneously. These solutions represent the points of intersection if the equations were graphed.
The elimination method, also known as the addition method, is a powerful technique for solving systems of equations. It involves manipulating the equations to eliminate one variable, leaving a single equation with one variable that can be easily solved. Once one variable is solved, its value is substituted back into one of the original equations to find the value of the other variable.
Steps in the Elimination Method:
-
Prepare the Equations: Ensure the equations are in standard form (Ax + By = C). You might need to rearrange equations or multiply them by constants to align coefficients.
-
Eliminate a Variable: Add or subtract the equations to eliminate one variable. The goal is to have opposite coefficients for one variable so that they cancel when added. For example, if you have 3x and -3x, they will eliminate when added together.
-
Solve for the Remaining Variable: After eliminating a variable, you'll have a single equation with one variable. Solve this equation to find the value of that variable.
-
Substitute and Solve: Substitute the value you found in step 3 into one of the original equations and solve for the remaining variable.
-
Check Your Solution: Substitute both values into both original equations to verify they satisfy both equations.
Using an Elimination Calculator: A Step-by-Step Guide
While the elimination method is straightforward for simple systems, more complex systems with many variables or complicated coefficients benefit greatly from the use of an elimination calculator. These online tools automate the process, reducing the chance of errors and saving significant time.
Although specific interfaces vary among calculators, the general process usually involves these steps:
-
Input the Equations: Enter your system of equations into the calculator's input fields. Ensure you accurately input the coefficients and constants for each variable. Most calculators will accept equations in standard form (Ax + By = C) or similar formats. Pay close attention to signs (+ or -).
-
Select the Method: Some calculators allow you to specify the solution method. Select "elimination" or "addition" as the preferred method.
-
Review the Output: The calculator will typically display the solution as an ordered pair (x, y) or a set of values for each variable in the system. The calculator will show the steps taken to reach the solution, allowing you to verify the process and understand how the elimination method was applied.
-
Verify the Solution (Crucial): Always verify the solution obtained from the calculator by manually substituting the values back into the original equations. This step is crucial to ensure accuracy and catch any potential errors. Even the best calculators can malfunction or misinterpret the input.
Handling Special Cases: Inconsistent and Dependent Systems
Not all systems of equations have a unique solution. An elimination calculator can help identify these special cases:
1. Inconsistent Systems: These systems have no solution. When attempting to solve an inconsistent system using the elimination method, you'll arrive at a contradictory statement, such as 0 = 5. An elimination calculator will often indicate "no solution" or a similar message in these cases. Graphically, the lines represented by the equations are parallel and never intersect.
2. Dependent Systems: These systems have infinitely many solutions. When solving a dependent system using elimination, you'll obtain an identity, such as 0 = 0. This signifies that the equations are essentially equivalent or multiples of each other. An elimination calculator might express the solution in parametric form, indicating a family of solutions. Graphically, the lines represented by the equations overlap completely.
Advanced Applications and Extensions
The elimination method and elimination calculators extend beyond simple two-variable systems. They can be used to solve:
-
Systems with Three or More Variables: The principle remains the same, but the process becomes more involved. Elimination calculators are invaluable in these situations, significantly simplifying the calculations and reducing the chance of errors.
-
Matrix Representation: Systems of equations can be represented using matrices, providing a compact and efficient way to express and solve them. Many elimination calculators also support matrix input, allowing for the solution of large systems using matrix operations.
-
Applications in Linear Programming: The elimination method forms the basis of several algorithms used in linear programming, a technique for optimizing objective functions subject to constraints.
-
Solving Systems of Non-linear Equations (Approximation): While the elimination method is primarily for linear systems, numerical methods based on similar principles can approximate solutions for non-linear systems. Some advanced calculators might offer such functionality.
Tips for Effective Use of Elimination Calculators
-
Accurate Input: Double-check your input values carefully before submitting them to the calculator. A small error in input can lead to an incorrect solution.
-
Understand the Process: Don't just rely on the calculator; try to understand the steps it takes to solve the system. This will enhance your understanding of the elimination method and improve your problem-solving skills.
-
Multiple Calculators: Consider using multiple calculators to verify results, as different calculators may employ slightly different algorithms and have varying degrees of accuracy.
-
Explore Different Interfaces: Various online elimination calculators exist, each with its own interface and features. Experiment to find one that suits your preferences and provides the information you need.
-
Practice Regularly: Consistent practice is key to mastering the elimination method and effectively using an elimination calculator. Start with simple systems and gradually increase the complexity.
Conclusion: Empowering Problem-Solving with Technology
Solving systems of equations is a crucial skill in various disciplines. The elimination method provides a systematic approach, and elimination calculators offer an efficient tool for solving even complex systems. By understanding the underlying principles and effectively using calculators, you can significantly improve your problem-solving abilities and tackle challenging mathematical problems with confidence. Remember to always verify your results manually to ensure accuracy and build a strong conceptual understanding. The combination of manual problem-solving skills and the assistance of technology offers a powerful approach to mastering systems of equations.
Latest Posts
Latest Posts
-
How Many Pounds In 92 Kilos
Apr 02, 2025
-
How Big Is 22cm In Inches
Apr 02, 2025
-
How Many Pounds Is 177 Kilos
Apr 02, 2025
-
How Many Feet Is 139 Inches
Apr 02, 2025
-
140 Km Is How Many Miles
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Solve The System Of Equations Using Elimination Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
