Solve The System Of Equations By Elimination Calculator
Greels
Apr 01, 2025 · 6 min read
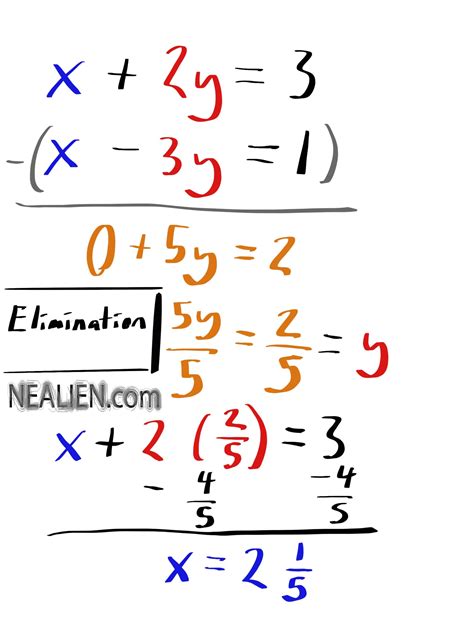
Table of Contents
Solve the System of Equations by Elimination Calculator: A Comprehensive Guide
Solving systems of equations is a fundamental concept in algebra, with applications spanning various fields like physics, engineering, and economics. While solving these systems manually can be time-consuming and prone to errors, especially with complex equations, using a system of equations by elimination calculator offers a streamlined and accurate approach. This comprehensive guide dives deep into the elimination method, explores its applications, and provides a detailed understanding of how a calculator can simplify the process.
Understanding the Elimination Method
The elimination method, also known as the addition method, is a powerful algebraic technique used to solve systems of linear equations. The core idea is to manipulate the equations strategically so that when they're added together, one of the variables cancels out, leaving a single equation with one variable that can be easily solved. Once this value is found, it can be substituted back into either of the original equations to solve for the remaining variable.
Let's illustrate with a simple example:
Solve the system of equations:
- 2x + y = 7
- x - y = 2
Step 1: Identify a variable to eliminate. Notice that the 'y' terms have opposite signs (+y and -y). This is ideal for elimination.
Step 2: Add the equations together. Adding the equations directly eliminates 'y':
(2x + y) + (x - y) = 7 + 2
This simplifies to:
3x = 9
Step 3: Solve for the remaining variable. Dividing both sides by 3 gives:
x = 3
Step 4: Substitute the value back into one of the original equations. Let's use the first equation:
2(3) + y = 7
This simplifies to:
6 + y = 7
Solving for 'y' gives:
y = 1
Therefore, the solution to the system of equations is x = 3 and y = 1.
When Elimination Method Might Be Difficult
While the elimination method is efficient for many systems, certain situations can make it more challenging:
- No readily eliminable variables: If none of the variables have coefficients that are opposites or easily made into opposites through multiplication, additional steps are needed to manipulate the equations.
- Fractions or decimals: Equations involving fractions or decimals can complicate the process and increase the likelihood of errors during manual calculations.
- Large coefficients: Equations with large coefficients can lead to complex calculations, making the process tedious and error-prone.
This is where a system of equations by elimination calculator becomes invaluable. It automates these steps, eliminating the manual effort and significantly reducing the risk of errors, especially when dealing with complex systems.
Utilizing a System of Equations by Elimination Calculator
A system of equations by elimination calculator simplifies the process by automating the steps involved. Generally, you input the equations into the calculator, specifying the coefficients for each variable and the constant terms. The calculator then performs the following functions:
- Identifies the most efficient elimination strategy: The calculator analyzes the coefficients to determine the optimal approach for eliminating a variable, minimizing the number of steps required.
- Performs the necessary multiplications: It multiplies equations by appropriate constants to create coefficients that will eliminate a variable upon addition.
- Adds the equations: It accurately adds the modified equations, eliminating one of the variables.
- Solves for the remaining variable: It solves the resulting single-variable equation.
- Substitutes and solves for the second variable: It substitutes the solved value back into an original equation to find the value of the second variable.
- Displays the solution: The calculator presents the solution in a clear and easily understandable format, typically displaying the values of both variables.
Many online calculators also provide step-by-step solutions, allowing users to understand the process even if they aren't comfortable performing the calculations manually. This feature is particularly useful for educational purposes or for those wanting to verify their manual calculations.
Beyond Simple Linear Equations: Expanding Capabilities
While basic elimination calculators handle systems of two linear equations with two variables, more advanced calculators can handle:
- Systems with three or more variables: Solving systems with three or more variables manually is significantly more challenging. A calculator extends the elimination method to handle these complex systems efficiently.
- Non-linear equations: Although less common, some calculators can address systems involving non-linear equations, requiring more sophisticated algorithms to find solutions. These often involve iterative methods that approximate solutions.
- Matrix representation: Some calculators utilize matrix operations to solve systems of equations, offering a concise and efficient representation, particularly helpful for larger systems.
This enhanced functionality makes these calculators indispensable tools for advanced mathematical applications and research.
Applications of Solving Systems of Equations
The applications of solving systems of equations are vast and permeate various disciplines:
- Physics and Engineering: Solving circuit problems, determining forces in equilibrium, and analyzing mechanical systems all require solving systems of equations.
- Economics and Finance: Modeling economic relationships, predicting market trends, and optimizing investment portfolios often involve analyzing systems of equations.
- Computer Science: Algorithms in computer graphics, game development, and machine learning frequently rely on solving systems of equations.
- Chemistry and Biology: Analyzing chemical reactions, modeling biological processes, and studying population dynamics often utilize systems of equations.
Choosing the Right Calculator
When selecting a system of equations by elimination calculator, several factors should be considered:
- Functionality: Determine the type of equations the calculator can handle (linear, non-linear, number of variables).
- User interface: A user-friendly interface is crucial for ease of use, especially for beginners. Look for clear instructions and easy input methods.
- Step-by-step solutions: The ability to see step-by-step solutions is invaluable for understanding the process and checking for errors.
- Accuracy: Ensure the calculator provides accurate results, especially when dealing with complex systems.
Tips for Effective Use
To maximize the effectiveness of a system of equations by elimination calculator:
- Double-check your input: Carefully verify that the coefficients and constants are correctly entered into the calculator to avoid errors.
- Understand the output: Familiarize yourself with the calculator's output format to correctly interpret the solution.
- Use for verification: Even if proficient in manual calculation, use the calculator to verify your answers and catch potential errors.
- Explore advanced features: If the calculator offers additional features like matrix operations or step-by-step explanations, take advantage of them to enhance your understanding and problem-solving skills.
Conclusion
Solving systems of equations by elimination is a critical skill in various fields. While manual calculation can be effective for simple systems, utilizing a system of equations by elimination calculator significantly improves efficiency, reduces errors, and enables the solution of more complex problems. By selecting a calculator with appropriate functionality and understanding its features, users can leverage this powerful tool to streamline their problem-solving process and unlock new opportunities in their respective domains. The right calculator becomes an invaluable asset for students, researchers, and professionals alike, facilitating accurate and efficient solutions to even the most intricate systems of equations.
Latest Posts
Latest Posts
-
How Many Feet Is 146 Inches
Apr 02, 2025
-
How Many Lbs Is 150 Grams
Apr 02, 2025
-
What Is 106 Cm In Inches
Apr 02, 2025
-
What Is 8 11 As A Decimal
Apr 02, 2025
-
2c 3 2 6 C 7c
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Solve The System Of Equations By Elimination Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
