Solve The System By Elimination Calculator
Greels
Apr 04, 2025 · 6 min read
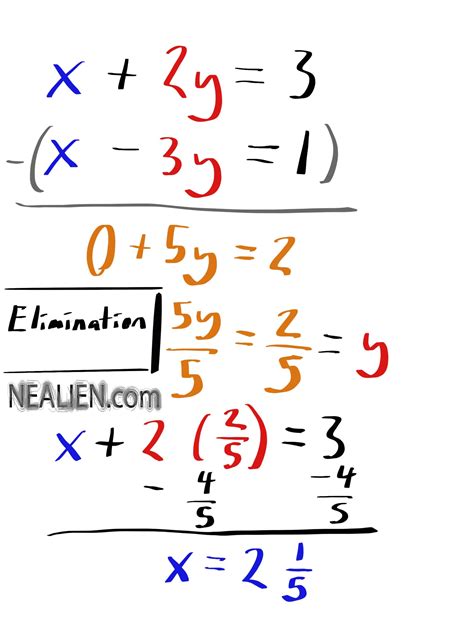
Table of Contents
Solve the System by Elimination Calculator: A Comprehensive Guide
Solving systems of linear equations is a fundamental concept in algebra with wide-ranging applications in various fields, from physics and engineering to economics and computer science. While manual calculation is possible, utilizing a system of equations calculator, particularly one employing the elimination method, significantly streamlines the process and minimizes the risk of human error. This comprehensive guide will delve into the elimination method, explain how a solve the system by elimination calculator works, explore its benefits, and offer valuable tips for effective usage.
Understanding the Elimination Method
The elimination method, also known as the addition method, is a powerful technique for solving systems of linear equations. Its core principle lies in manipulating the equations to eliminate one variable, thereby reducing the system to a single equation with one variable that can be easily solved. Once this variable's value is determined, it's substituted back into one of the original equations to find the value of the remaining variable.
Let's illustrate with a simple example:
Example:
Solve the following system of equations using the elimination method:
Equation 1: 2x + y = 7 Equation 2: x - y = 2
Steps:
-
Identify the variable to eliminate: In this case, the 'y' variable has opposite signs in both equations (+y and -y). This makes elimination straightforward.
-
Add the equations: Adding Equation 1 and Equation 2 directly eliminates 'y':
(2x + y) + (x - y) = 7 + 2
This simplifies to: 3x = 9
-
Solve for x: Dividing both sides by 3, we get x = 3.
-
Substitute and solve for y: Substitute the value of x (3) into either Equation 1 or Equation 2. Let's use Equation 1:
2(3) + y = 7
6 + y = 7
y = 1
Therefore, the solution to the system of equations is x = 3 and y = 1.
The Role of a Solve the System by Elimination Calculator
While the elimination method is relatively simple for small systems, it becomes significantly more complex and prone to errors with larger systems or those involving more intricate coefficients. This is where a solve the system by elimination calculator proves invaluable. These calculators automate the entire process, eliminating the need for manual calculations and reducing the chance of mistakes.
A typical solve the system by elimination calculator will:
-
Accept input: You input the system of equations, typically in the standard form (ax + by = c). The calculator may support various input formats, and you should understand how your chosen calculator requires you to enter the equations.
-
Perform elimination: The calculator uses algorithms based on the elimination method to manipulate the equations. This might involve multiplying equations by constants to create opposites for elimination. More advanced calculators might use Gaussian elimination, a more sophisticated version of the elimination method designed to work with larger systems efficiently.
-
Solve for variables: The calculator determines the values of the variables that satisfy the system of equations.
-
Provide output: The calculator displays the solution, usually listing the values of all the variables. It may also provide a graphical representation of the solution, showing the intersection point of the lines represented by the equations (if dealing with a two-variable system).
Benefits of Using a Solve the System by Elimination Calculator
There are several compelling reasons to leverage a solve the system by elimination calculator:
-
Accuracy: Manual calculations are susceptible to errors, especially with complex systems. A calculator eliminates this risk, ensuring accurate results.
-
Efficiency: The calculator dramatically reduces the time required to solve a system of equations, allowing you to focus on other aspects of your problem or assignment.
-
Ease of use: Even without advanced mathematical knowledge, anyone can use a solve the system by elimination calculator to obtain accurate solutions.
-
Educational tool: The calculator can be a valuable educational tool, assisting in understanding the elimination method and verifying manually calculated solutions. It provides instantaneous feedback, helping students identify where their calculations went wrong.
-
Handling complex systems: Solving large systems of equations manually is extremely tedious and time-consuming. A calculator effortlessly handles such complex scenarios.
Choosing the Right Solve the System by Elimination Calculator
Several online calculators and software programs offer the ability to solve systems of equations using the elimination method. When selecting a calculator, consider these factors:
-
Ease of use: The interface should be intuitive and user-friendly, enabling effortless input of equations.
-
Accuracy: Verify the calculator's accuracy by testing it with simple systems that you can solve manually to compare the outputs.
-
Features: Look for calculators that can handle a large number of equations and variables. Some may offer additional features such as graphing capabilities or step-by-step solution explanations, which can be particularly useful for educational purposes.
-
Accessibility: Ensure the calculator is readily available and accessible when you need it. Online calculators are generally more convenient than software that needs to be downloaded and installed.
Advanced Applications and Extensions
The elimination method and its computational implementation are not just limited to simple linear equations. Extensions and adaptations of this method are employed in more advanced scenarios:
-
Gaussian Elimination: This is a systematic algorithm that extends the elimination method to solve larger systems of linear equations, often represented in matrix form. It's a cornerstone algorithm in linear algebra and numerical analysis.
-
Solving systems of non-linear equations: While the elimination method is primarily suited for linear equations, numerical methods inspired by the elimination method can be adapted to approximate solutions for systems of non-linear equations.
-
Linear Programming: Optimization problems involving linear objective functions and linear constraints often employ variations of the elimination method (like the simplex method) to find optimal solutions.
-
Computer Graphics and Simulations: Solving systems of equations is vital in computer graphics to render realistic images and simulations. Efficient algorithms based on elimination are essential for real-time applications.
Tips for Effective Use of a Solve the System by Elimination Calculator
To maximize the benefits of using a solve the system by elimination calculator, consider these tips:
-
Double-check your input: Carefully review the equations you input into the calculator to ensure accuracy. A single misplaced number or incorrect sign can lead to an entirely wrong solution.
-
Understand the output: After obtaining the solution, verify that it satisfies all equations in the system. Substitute the values into the original equations to confirm that they hold true.
-
Use the calculator as a tool, not a crutch: The calculator should enhance your understanding, not replace it. It is crucial to grasp the underlying principles of the elimination method to interpret the results meaningfully and identify potential errors.
-
Explore advanced features: Many calculators offer additional features like step-by-step solutions or graphing capabilities. Utilize these features to deepen your understanding and gain insights into the solution process.
-
Practice with various examples: Work through various examples of increasing complexity to build your proficiency with both the manual method and the calculator. This will help you identify situations where the calculator is particularly useful.
Conclusion: Empowering Problem-Solving with Technology
A solve the system by elimination calculator is a powerful tool that significantly improves the efficiency and accuracy of solving systems of linear equations. By understanding its functionality and implementing the tips outlined above, you can effectively leverage its capabilities to solve complex problems and enhance your mathematical understanding. While it’s crucial to learn the underlying principles of the elimination method, the calculator offers a valuable supplement, reducing the burden of manual computation and enabling you to focus on the broader context and application of the solution. It’s a testament to how technology can empower problem-solving and elevate our abilities in mathematics and beyond.
Latest Posts
Latest Posts
-
Parallel And Perpendicular Line Equation Calculator
Apr 05, 2025
-
7b 2 5 6b 7 5
Apr 05, 2025
-
How Many Inches Is 169 Cm
Apr 05, 2025
-
How Many Inches In 48 Mm
Apr 05, 2025
-
85 Km Is How Many Miles
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Solve The System By Elimination Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
