Simplify To A Single Trig Function Without Denominator
Greels
Mar 25, 2025 · 5 min read
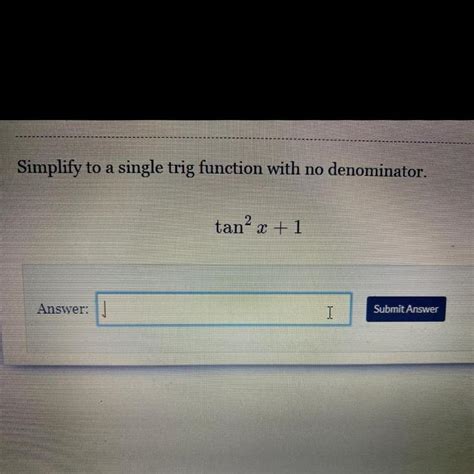
Table of Contents
- Simplify To A Single Trig Function Without Denominator
- Table of Contents
- Simplify to a Single Trig Function Without Denominator
- Understanding Fundamental Trigonometric Identities
- Reciprocal Identities:
- Quotient Identities:
- Pythagorean Identities:
- Strategies for Simplification
- 1. Utilizing Reciprocal and Quotient Identities:
- 2. Factoring and Cancellation:
- 3. Applying Pythagorean Identities Strategically:
- 4. Using Angle Sum and Difference Identities:
- 5. Double Angle and Half Angle Formulas:
- Advanced Examples and Challenges
- Conclusion: Mastering Trigonometric Simplification
- Latest Posts
- Latest Posts
- Related Post
Simplify to a Single Trig Function Without Denominator
Simplifying trigonometric expressions is a fundamental skill in mathematics, particularly crucial for calculus, physics, and engineering. Often, we encounter expressions involving multiple trigonometric functions and denominators, making them cumbersome to work with. This article delves into the techniques for simplifying trigonometric expressions to a single trigonometric function without a denominator. We’ll explore various identities and strategies, providing ample examples to solidify your understanding.
Understanding Fundamental Trigonometric Identities
Before we begin simplifying, it's essential to review the core trigonometric identities. These identities form the bedrock of our simplification process. Mastering them is key to efficiently tackling complex expressions.
Reciprocal Identities:
- csc θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
These identities allow us to replace fractions involving sine, cosine, and tangent with their reciprocal counterparts, often simplifying the expression.
Quotient Identities:
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
These identities are crucial for converting between tangent, cotangent, sine, and cosine, offering flexibility in our simplification approach.
Pythagorean Identities:
- sin² θ + cos² θ = 1
- 1 + tan² θ = sec² θ
- 1 + cot² θ = csc² θ
These identities are powerful tools for eliminating squared trigonometric functions or expressing one trigonometric function in terms of another. They're frequently used to substitute and simplify expressions.
Strategies for Simplification
Now, let's examine effective strategies to simplify trigonometric expressions into a single trigonometric function without a denominator.
1. Utilizing Reciprocal and Quotient Identities:
This is often the first step. Replace fractions with their reciprocal functions to eliminate obvious denominators. Then, apply the quotient identities to express everything in terms of sine and cosine.
Example:
Simplify (sin θ / cos θ) + (cos θ / sin θ)
- Recognize the Quotient Identities: We can rewrite this as
tan θ + cot θ. - Express in terms of sine and cosine: This becomes
(sin θ / cos θ) + (cos θ / sin θ). - Find a common denominator:
(sin² θ + cos² θ) / (sin θ cos θ) - Apply Pythagorean Identity: Since
sin² θ + cos² θ = 1, the expression simplifies to1 / (sin θ cos θ). - Further Simplification (Optional): While this is a single function, it still has a denominator. To remove the denominator and express it as a single function might require more information or context about the problem. For example, if we know that the angle θ is such that sin θ cos θ = 1/2 (e.g., θ = π/4), then we can simplify to 2. But without specific conditions, this remains the most simplified form within the constraint.
2. Factoring and Cancellation:
Often, trigonometric expressions can be factored, allowing for cancellation of terms. Look for common factors, particularly those that allow us to apply Pythagorean identities to simplify further.
Example:
Simplify sin² θ - cos² θ
- Recognize the difference of squares: This can be factored as
(sin θ + cos θ)(sin θ - cos θ). - Further Simplification: Without additional constraints, this is the most simplified factored form. It's a product of two trigonometric functions. However, we can express it differently using other identities. For instance, we know that
sin² θ - cos² θ = -cos(2θ), offering a form with a single function. Therefore, the 'single trig function' aspect also depends heavily on the form the question requires.
3. Applying Pythagorean Identities Strategically:
Pythagorean identities are immensely powerful. Use them to replace expressions containing squared trigonometric functions, or to express one trigonometric function in terms of another. This can lead to simplification and the elimination of denominators.
Example:
Simplify (1 - sin² θ) / cos² θ
- Apply Pythagorean Identity: We know that
1 - sin² θ = cos² θ. - Substitute and Simplify: The expression becomes
cos² θ / cos² θ, which simplifies to 1. This is a single trigonometric function (although a constant one).
4. Using Angle Sum and Difference Identities:
Angle sum and difference identities can be used to combine multiple trigonometric functions into a single term, sometimes eliminating denominators.
Example: Simplify sin(x+y) + sin(x-y). Using the angle sum and difference identities, we have: sin(x+y) = sinxcosy + cosxsiny sin(x-y) = sinxcosy - cosxsiny Adding these together, we get: 2sinxcosy. This simplifies to a single trigonometric function without a denominator, but it involves a combination of sinx and cosy rather than a single variable.
5. Double Angle and Half Angle Formulas:
These formulas are crucial for converting between angles and simplifying expressions. Mastering them expands your ability to manipulate and simplify complex trigonometric expressions. Especially for simplifying expressions involving powers of trigonometric functions.
Example:
Simplify 2sin θ cos θ
- Recognize the Double Angle Identity: This is equal to
sin(2θ).
Advanced Examples and Challenges
Let's tackle more intricate examples to further illustrate these techniques.
Example 1: Simplify (tan θ + cot θ) / (sec² θ)
- Express in terms of sine and cosine: This becomes
[(sin θ / cos θ) + (cos θ / sin θ)] / (1 / cos² θ). - Find a common denominator for the numerator:
[(sin² θ + cos² θ) / (sin θ cos θ)] / (1 / cos² θ) - Simplify the numerator using Pythagorean Identity: This simplifies to
[1 / (sin θ cos θ)] / (1 / cos² θ) - Simplify the complex fraction: This becomes
cos² θ / (sin θ cos θ) = cos θ / sin θ = cot θ
Example 2: Simplify (sin² x + cos² x)/(1 - sin² x)
- Apply Pythagorean identity: The numerator is 1.
- Apply Pythagorean Identity to the denominator: 1 - sin²x = cos²x.
- Simplify: 1/cos²x = sec²x
These advanced examples highlight the importance of a systematic approach. Remember to break down the expression into smaller, manageable parts, consistently applying relevant identities.
Conclusion: Mastering Trigonometric Simplification
Simplifying trigonometric expressions to a single function without a denominator requires a thorough understanding of fundamental identities, strategic application of these identities, and practice. By mastering these techniques, you'll significantly improve your problem-solving skills in mathematics, particularly in calculus-based subjects and related fields. Remember that the ability to express a trigonometric function as a single term, without a denominator, depends on both the initial expression and the allowable manipulation. Sometimes a simplified expression may still have a denominator, representing the most simplified form given the constraints. The key is always to apply identities strategically to obtain the simplest possible representation.
Latest Posts
Latest Posts
-
How Many Feet Is 10000 Meters
Mar 28, 2025
-
What Is 38 Inches In Cm
Mar 28, 2025
-
How Many Pounds Is 5000 Grams
Mar 28, 2025
-
63 Kilos Is How Many Pounds
Mar 28, 2025
-
What Is 80 Percent Of 40
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Simplify To A Single Trig Function Without Denominator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
