Simplify The Expression To A Bi Form
Greels
Mar 27, 2025 · 5 min read
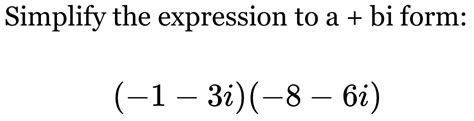
Table of Contents
Simplifying Expressions to a Bi-Form: A Comprehensive Guide
The concept of simplifying expressions to a "bi-form" isn't a standard mathematical term. It's likely referring to expressing an expression in a form involving two distinct parts, often a real part and an imaginary part (in the context of complex numbers), or a constant term and a variable term (in the context of algebraic expressions). This guide will cover both scenarios, providing a comprehensive understanding of simplification techniques applicable in various mathematical domains. We'll focus on strategies to simplify expressions, emphasizing step-by-step methods and practical examples to solidify your understanding.
Simplifying Expressions with Real and Imaginary Parts (Complex Numbers)
When dealing with complex numbers, the "bi-form" likely refers to the standard form: a + bi, where 'a' represents the real part and 'b' represents the imaginary part, with 'i' being the imaginary unit (√-1). Simplifying complex number expressions means manipulating them to arrive at this standard form.
Essential Techniques for Simplifying Complex Numbers
-
Distributive Property: This is fundamental when dealing with expressions involving parentheses. Remember that
iacts like any other variable, obeying the rules of algebra. For example:2(3 + 4i) = 6 + 8i -
Combining Like Terms: Just like in regular algebra, you can combine terms with real parts together and imaginary parts together. For example:
(2 + 3i) + (5 - 2i) = (2 + 5) + (3 - 2)i = 7 + i -
Dealing with Powers of i: The powers of i cycle:
i¹ = ii² = -1i³ = -ii⁴ = 1i⁵ = iand so on...
This cyclic property is crucial for simplifying expressions involving higher powers of i. For instance:
5i³ + 2i⁵ = 5(-i) + 2(i) = -5i + 2i = -3i -
Complex Conjugates: The complex conjugate of a complex number
a + biisa - bi. Multiplying a complex number by its conjugate eliminates the imaginary part, resulting in a real number. This technique is vital for simplifying expressions involving division of complex numbers. For example:To simplify
(2 + 3i) / (1 - i), we multiply both the numerator and denominator by the conjugate of the denominator (1 + i):[(2 + 3i)(1 + i)] / [(1 - i)(1 + i)] = (2 + 2i + 3i + 3i²) / (1 - i²)= (2 + 5i - 3) / (1 + 1) = (-1 + 5i) / 2 = -1/2 + (5/2)i
Worked Examples: Simplifying Complex Number Expressions
Example 1: Simplify (4 + 2i) - (1 - 3i) + 5i²
- Distribute the negative sign:
4 + 2i - 1 + 3i + 5i² - Substitute
i² = -1:4 + 2i - 1 + 3i - 5 - Combine like terms:
(4 - 1 - 5) + (2 + 3)i = -2 + 5i
Example 2: Simplify (3 + i)(2 - 4i)
- Use the FOIL method (First, Outer, Inner, Last):
(3)(2) + (3)(-4i) + (i)(2) + (i)(-4i) - Simplify:
6 - 12i + 2i - 4i² - Substitute
i² = -1:6 - 10i + 4 - Combine like terms:
10 - 10i
Example 3: Simplify (5 + 2i) / (3 + i)
-
Multiply the numerator and denominator by the conjugate of the denominator (3 - i):
[(5 + 2i)(3 - i)] / [(3 + i)(3 - i)] -
Expand the numerator and denominator:
(15 - 5i + 6i - 2i²) / (9 - 3i + 3i - i²) -
Simplify and substitute
i² = -1:(15 + i + 2) / (9 + 1) = (17 + i) / 10 -
Write in standard form:
17/10 + (1/10)i
Simplifying Algebraic Expressions to a "Bi-Form" (Constant and Variable Terms)
In algebra, simplifying an expression to a "bi-form" might mean separating it into a constant term and a variable term. This is particularly useful when solving equations or performing other algebraic manipulations.
Techniques for Separating Constant and Variable Terms
-
Distributive Property: This is crucial for expanding expressions and revealing the constant and variable components.
-
Combining Like Terms: Group terms with the same variables together.
-
Factoring: Factor out common factors to simplify expressions and isolate the constant term from the variable terms. For example,
2x + 4can be factored as2(x + 2). While this doesn't strictly separate them into distinct constant and variable components, it simplifies the expression in a meaningful "bi-like" fashion. -
Rearrangement: Simply rearrange the terms to group constants and variable terms together.
Worked Examples: Separating Constant and Variable Terms
Example 1: Simplify and express 3x + 5 - 2x + 1 in a bi-form.
- Combine like terms:
(3x - 2x) + (5 + 1) - Simplify:
x + 6This is now in a bi-form: a variable term (x) and a constant term (6).
Example 2: Simplify and express 2(x + 3) - 4x + 7 in a bi-form.
- Distribute the 2:
2x + 6 - 4x + 7 - Combine like terms:
(2x - 4x) + (6 + 7) - Simplify:
-2x + 13This is in a bi-form: a variable term (-2x) and a constant term (13).
Example 3: Simplify and express (x + 2)(x - 1) + 5
- Expand using the FOIL method:
x² - x + 2x - 2 + 5 - Combine like terms:
x² + x + 3While not strictly in a "constant and variable" form due to the quadratic term, it's a simplified form showing a quadratic term and a linear term with a constant added.
Example 4: Simplify and express 4x² + 6x - 8
This is already in a fairly simplified form. One could factor out a common factor of 2: 2(2x² + 3x - 4). This representation gives some separation, showing a constant multiplier (2) and a variable expression (2x² + 3x - 4). However, it doesn't explicitly separate into just a constant and a variable term.
Beyond the "Bi-Form": Further Simplification Techniques
The concept of simplifying to a "bi-form" provides a useful framework, but remember that simplification often involves broader strategies depending on the context:
- Factoring: Breaking down expressions into simpler multiplicative components.
- Expanding: Removing parentheses by distributing terms.
- Cancelling Common Factors: Simplifying fractions by removing common factors from the numerator and denominator.
- Rationalizing the Denominator: Removing radicals from the denominator of a fraction.
By mastering these techniques, you'll be well-equipped to simplify a wide range of mathematical expressions, significantly improving your problem-solving abilities. Remember to always check your work for accuracy and strive for the simplest possible representation of the expression. The key is understanding the underlying principles of algebra and applying the appropriate techniques strategically. Practice is key to developing proficiency in simplifying expressions.
Latest Posts
Latest Posts
-
89 Centimeters Is How Many Inches
Mar 30, 2025
-
How Many Pounds In 96 Ounces
Mar 30, 2025
-
How Long Is 17 Inches In Cm
Mar 30, 2025
-
What Day Will It Be In 22 Days
Mar 30, 2025
-
What Is 81 Kilos In Pounds
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Expression To A Bi Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
