Simplify 1 X 1 1 X
Greels
Apr 03, 2025 · 5 min read
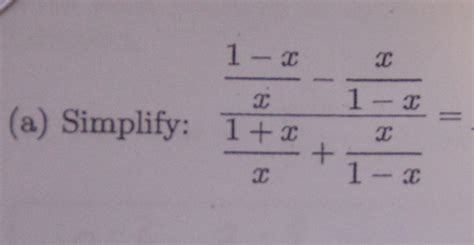
Table of Contents
Simplify 1 x 1 1 x: A Deep Dive into the Fundamentals of Multiplication and its Applications
The seemingly simple expression "1 x 1 1 x" might appear trivial at first glance. However, a closer examination reveals core concepts within mathematics, specifically multiplication, and its wide-ranging applications across various fields. This article will delve into the simplification of this expression, explore the fundamental principles behind multiplication, and discuss its relevance in real-world scenarios, from basic arithmetic to complex computations.
Understanding the Fundamentals: What is Multiplication?
Multiplication, at its core, is a form of repeated addition. When we say "1 x 1," we are essentially asking, "What is the sum of one '1' repeated one time?" The answer, obviously, is 1. This fundamental concept forms the basis of all multiplication operations, no matter how complex they become.
The Commutative Property: Order Doesn't Matter (Usually)
One crucial property of multiplication is its commutativity. This means the order of the numbers being multiplied doesn't affect the result. For example, 2 x 3 is the same as 3 x 2; both equal 6. This property holds true for our initial expression, "1 x 1 1 x." Regardless of how we group or arrange the '1's, the outcome remains unchanged.
The Identity Property of 1: The Multiplicative Neutral Element
The number '1' holds a special position in multiplication. It's known as the multiplicative identity, meaning that any number multiplied by 1 remains unchanged. This property is vital in simplifying expressions. In our case, "1 x 1 1 x," each '1' acts as a multiplicative identity, leaving the overall product unaffected.
Simplifying "1 x 1 1 x": A Step-by-Step Approach
Let's systematically simplify the expression "1 x 1 1 x." There are several ways to approach this, all leading to the same answer:
-
Method 1: Sequential Multiplication: We can multiply the numbers sequentially from left to right.
- 1 x 1 = 1
- 1 x 1 = 1 (The second '1' remains unchanged since it's multiplied by 1)
- Therefore, the expression simplifies to 1.
-
Method 2: Grouping and Multiplication: We can group the numbers using parentheses to clarify the order of operations. Although not strictly necessary in this simple case, it's good practice for more complex expressions.
- (1 x 1) x (1 x 1) = 1 x 1 = 1
-
Method 3: Applying the Identity Property: We can immediately recognize that every number in the expression is '1.' Since multiplying by '1' doesn't change the value, the final result is simply '1.'
Regardless of the chosen method, the simplified form of "1 x 1 1 x" is 1.
Beyond the Basics: Multiplication in Different Contexts
While the simplification of "1 x 1 1 x" is straightforward, the underlying principles of multiplication have far-reaching implications:
1. Algebra: The Foundation of Equations
Multiplication is fundamental to algebra. Variables are often combined using multiplication to express relationships between different quantities. For instance, the area of a rectangle is calculated as length x width. Understanding multiplication is crucial for solving algebraic equations and manipulating expressions.
2. Geometry: Calculating Areas and Volumes
In geometry, multiplication plays a pivotal role in calculating areas and volumes of various shapes. The area of a square is side x side, the volume of a cube is side x side x side, and so on. The ability to perform multiplications accurately is essential for geometrical calculations.
3. Physics: Describing Motion and Forces
Multiplication finds widespread application in physics, especially when dealing with motion, forces, and energy. Calculating velocity (speed x time), force (mass x acceleration), and work (force x distance) all require the use of multiplication.
4. Computer Science: Binary Operations and Data Structures
In computer science, binary operations – operations on binary numbers – often involve multiplication. Data structures like arrays and matrices rely heavily on multiplicative principles for efficient manipulation and access.
5. Finance: Calculating Interest and Investments
In finance, multiplication is crucial for calculating interest, compound interest, and the future value of investments. Understanding multiplication is essential for financial planning and investment strategies.
6. Everyday Life: Counting and Measurement
Even in our daily lives, we implicitly use multiplication countless times. Counting objects arranged in rows and columns, determining the total cost of multiple items, and measuring quantities all involve multiplication in some form.
Advanced Applications: Matrices and Beyond
The concept of multiplication extends far beyond simple whole numbers. In linear algebra, matrix multiplication is a complex operation with significant applications in computer graphics, data analysis, and machine learning. Matrices represent large sets of data, and their multiplication allows for efficient transformations and calculations.
Further extending the scope, multiplication finds its place in calculus, where it's used in differentiation, integration, and in dealing with infinite series and limits. These advanced concepts have applications in fields like physics, engineering, and economics, for modeling complex systems and phenomena.
Error Handling and Potential Pitfalls
While the example "1 x 1 1 x" is relatively simple, there are potential pitfalls when dealing with more complex multiplication problems:
-
Order of Operations: Following the correct order of operations (PEMDAS/BODMAS) is crucial for accurate results, especially when dealing with multiple operations (addition, subtraction, division, exponents, etc.). Ignoring the order can lead to significant errors.
-
Significant Figures: In scientific and engineering calculations, it is essential to account for significant figures. Rounding off numbers during intermediate steps can cause a propagation of errors in the final answer.
-
Handling Zero: Multiplying any number by zero always results in zero. This is a fundamental property that must be considered in various calculations.
-
Negative Numbers: The multiplication of negative numbers follows specific rules. Remember that multiplying two negative numbers results in a positive number.
Conclusion: The Ubiquitous Nature of Multiplication
The seemingly trivial expression "1 x 1 1 x" serves as a gateway to understanding the fundamental importance of multiplication in mathematics and its widespread applications across various fields. From basic arithmetic to advanced mathematical concepts, multiplication forms the backbone of numerous calculations and processes. A thorough understanding of its principles and properties is essential for success in many disciplines, highlighting its enduring relevance and significance. Mastering multiplication is not merely about learning a basic operation; it's about gaining a foundational tool for problem-solving and critical thinking across a multitude of contexts.
Latest Posts
Latest Posts
-
How Many Kilos Is 132 Pounds
Apr 04, 2025
-
How Many Days Is 75 Days From Today
Apr 04, 2025
-
172 Cm Is How Many Inches
Apr 04, 2025
-
How Tall Is 2 06 Meters In Feet
Apr 04, 2025
-
What Is 39 Kilograms In Pounds
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Simplify 1 X 1 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
