Second Derivative Of Parametric Equations Calculator
Greels
Mar 28, 2025 · 5 min read
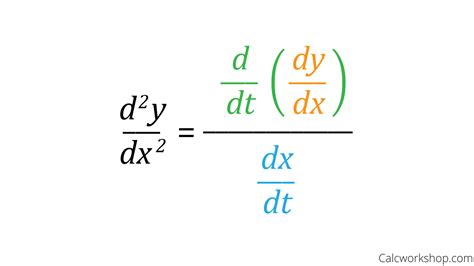
Table of Contents
Second Derivative of Parametric Equations Calculator: A Comprehensive Guide
Calculating the second derivative of parametric equations can be a complex process, prone to errors if done manually. Thankfully, with the advent of advanced calculators and computational tools, this task has become significantly easier and more accessible. This guide dives deep into understanding parametric equations, their derivatives, and the utilization of calculators to streamline the process. We will explore the theoretical underpinnings, practical applications, and address common challenges encountered while working with parametric second derivatives.
Understanding Parametric Equations
Before delving into the intricacies of calculating the second derivative, it's crucial to grasp the fundamental concept of parametric equations. Unlike Cartesian equations where 'y' is explicitly defined in terms of 'x' (e.g., y = x²), parametric equations represent a curve using a separate function for each coordinate, both dependent on a third variable, often denoted as 't' (parameter). This parameter represents a point on the curve.
A typical parametric equation set looks like this:
- x = f(t)
- y = g(t)
Here, 'x' and 'y' are dependent variables, and 't' is the independent parameter. The parameter 't' can represent time, angle, or any other independent variable. Changing the value of 't' traces out a path, forming the curve.
First Derivative of Parametric Equations
To find the first derivative, dy/dx, we utilize the chain rule:
dy/dx = (dy/dt) / (dx/dt)
This equation tells us that the rate of change of y with respect to x is the ratio of the rate of change of y with respect to t and the rate of change of x with respect to t. This gives us the slope of the tangent line to the curve at any given point 't'.
Second Derivative of Parametric Equations
Finding the second derivative, d²y/dx², requires a deeper understanding of derivative rules. It's not simply a matter of differentiating dy/dx directly with respect to x. Instead, we apply the quotient rule and chain rule strategically. The formula for the second derivative of parametric equations is:
d²y/dx² = [(d/dt)(dy/dx)] / (dx/dt)
Let's break this down:
-
Find dy/dx: As outlined above, calculate the first derivative using (dy/dt) / (dx/dt).
-
Differentiate dy/dx with respect to t: This step involves differentiating the expression obtained in step 1 with respect to 't'. This requires applying the quotient rule (or other relevant rules) for differentiation.
-
Divide by dx/dt: Finally, divide the result from step 2 by dx/dt. This gives the second derivative, d²y/dx².
Why Use a Calculator for Second Derivatives?
Manually computing the second derivative of parametric equations can be tedious and error-prone. The process involves multiple steps with potential for algebraic mistakes. A calculator, particularly one capable of symbolic differentiation, greatly simplifies this:
- Reduces Calculation Errors: Calculators minimize the risk of making errors during complex differentiation steps.
- Saves Time: The calculation process is significantly faster, allowing more time to focus on interpreting the results.
- Handles Complex Equations: Calculators can handle complicated parametric equations that would be extremely challenging to differentiate manually.
Using a Parametric Equation Calculator (Conceptual Steps)
While specific steps vary depending on the calculator, the general approach remains consistent:
-
Input the Parametric Equations: Enter the expressions for x = f(t) and y = g(t) into the calculator.
-
Specify the Differentiation Order: Indicate that you need the second derivative (d²y/dx²).
-
Specify the Variable: Identify the parameter 't'.
-
Obtain the Result: The calculator will compute and display the second derivative as a function of 't'.
-
Evaluate at Specific Points (Optional): Substitute specific values of 't' to find the second derivative at particular points along the curve. This helps determine concavity at various points.
Interpreting the Second Derivative
The second derivative, d²y/dx², provides crucial information about the curve:
- Concavity: A positive second derivative indicates concave up (like a U-shape), while a negative second derivative implies concave down (like an inverted U-shape).
- Inflection Points: Points where the concavity changes (from concave up to concave down or vice versa) are inflection points. These occur where the second derivative is zero or undefined.
- Curvature: The magnitude of the second derivative relates to the sharpness of the curve. A larger magnitude indicates a sharper curve.
Practical Applications of Parametric Second Derivatives
Parametric equations and their derivatives find applications in various fields:
-
Physics: Modeling projectile motion, analyzing particle trajectories, and studying oscillatory systems. The second derivative represents acceleration.
-
Engineering: Designing curves for roads and railways, optimizing shapes in structural designs, and analyzing the movement of robotic arms.
-
Computer Graphics: Creating smooth curves and surfaces for animation and modeling.
-
Economics: Analyzing changes in rates of growth or decay.
-
Biology: Modeling population dynamics and growth patterns.
Addressing Common Challenges
-
Dealing with Undefined Derivatives: If dx/dt becomes zero at some point, the second derivative will be undefined. This often indicates a vertical tangent at that point.
-
Complex Algebraic Simplification: The resulting expression for the second derivative might be complex and require significant simplification. Calculators often simplify results automatically, but an understanding of algebraic manipulation is still helpful.
-
Choosing the Right Calculator: Ensure that the calculator you choose is capable of symbolic differentiation and handles parametric equations effectively.
Conclusion
The second derivative of parametric equations offers valuable insights into the behavior of curves. While manual calculation can be intricate, utilizing a dedicated calculator or software simplifies the process significantly, allowing for accurate and efficient analysis. Understanding the theoretical basis and practical applications, along with the ability to interpret the results, empowers you to harness the power of parametric equations in a wide range of disciplines. Remember that accuracy is key, so double-check your inputs and understand the limitations of the calculator you are using. Always strive to verify your results through alternative methods or by checking for reasonableness within the context of the problem.
Latest Posts
Latest Posts
-
Cuanto Son 179 Libras En Kilos
Mar 31, 2025
-
How Many Kilograms Are In 125 Pounds
Mar 31, 2025
-
What Is 92 Days From Today
Mar 31, 2025
-
How Many Inches Is 240 Mm
Mar 31, 2025
-
26500 Km To Miles Per Hour
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Second Derivative Of Parametric Equations Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
