Rewrite The Given Equation Without Logarithms.
Greels
Apr 02, 2025 · 6 min read
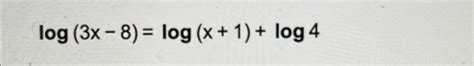
Table of Contents
Rewriting Equations Without Logarithms: A Comprehensive Guide
Logarithms, while powerful tools in mathematics and various scientific fields, can sometimes obscure the underlying relationships within an equation. Understanding how to rewrite equations without logarithms is crucial for simplification, better comprehension, and easier manipulation in certain contexts. This comprehensive guide will delve into various techniques and strategies for eliminating logarithms from equations, catering to different levels of mathematical understanding.
Understanding Logarithms: A Quick Recap
Before we embark on the process of removing logarithms, let's briefly revisit the fundamental definition. A logarithm is essentially the inverse operation of exponentiation. The equation log<sub>b</sub>(x) = y is equivalent to b<sup>y</sup> = x, where:
- b is the base of the logarithm (must be positive and not equal to 1).
- x is the argument (must be positive).
- y is the exponent or logarithm.
Common bases include base 10 (commonly written as log(x)) and base e (the natural logarithm, written as ln(x), where e ≈ 2.71828).
Techniques for Eliminating Logarithms
The method for rewriting an equation without logarithms depends heavily on the structure of the equation itself. Let's explore several common scenarios and their corresponding solutions.
1. Simple Logarithmic Equations
These are equations containing a single logarithmic term. The key here is to apply the definition of a logarithm to transform it into an exponential equation.
Example:
log<sub>2</sub>(x) = 3
Solution:
Using the definition, we rewrite this as:
2<sup>3</sup> = x
Therefore, x = 8.
2. Equations with Multiple Logarithmic Terms on the Same Side
If an equation has multiple logarithmic terms with the same base on one side, we can utilize the logarithm properties to combine them. Key properties include:
- Product Rule:
log<sub>b</sub>(xy) = log<sub>b</sub>(x) + log<sub>b</sub>(y) - Quotient Rule:
log<sub>b</sub>(x/y) = log<sub>b</sub>(x) - log<sub>b</sub>(y) - Power Rule:
log<sub>b</sub>(x<sup>p</sup>) = p * log<sub>b</sub>(x)
Example:
log<sub>10</sub>(x) + log<sub>10</sub>(x+1) = 1
Solution:
Using the product rule, we combine the logarithms:
log<sub>10</sub>(x(x+1)) = 1
Now, we convert to exponential form:
10<sup>1</sup> = x(x+1)
10 = x² + x
x² + x - 10 = 0
Solving this quadratic equation (e.g., using the quadratic formula) gives us the solutions for x. Remember to check for extraneous solutions – solutions that satisfy the rewritten equation but not the original logarithmic equation (due to restrictions on the argument of a logarithm being positive).
3. Equations with Logarithmic Terms on Both Sides
When logarithmic terms appear on both sides of the equation, and they share the same base, we can often eliminate the logarithms directly by equating the arguments.
Example:
log<sub>5</sub>(2x + 1) = log<sub>5</sub>(x + 4)
Solution:
Since the bases are the same, we can equate the arguments:
2x + 1 = x + 4
x = 3
Again, always verify that this solution doesn't violate the domain restrictions of the original logarithmic equation.
4. Equations with Logarithms and Other Terms
These equations require a more strategic approach. The goal is to isolate the logarithmic term(s) before converting to exponential form.
Example:
2log<sub>3</sub>(x) + 5 = 9
Solution:
First, isolate the logarithmic term:
2log<sub>3</sub>(x) = 4
log<sub>3</sub>(x) = 2
Now, convert to exponential form:
3<sup>2</sup> = x
x = 9
5. Equations Involving Natural Logarithms (ln)
Equations with natural logarithms follow the same principles, but the base is e.
Example:
ln(x) = 2
Solution:
This is equivalent to:
e<sup>2</sup> = x
x is approximately 7.389
6. Equations with Change of Base
Sometimes, you might encounter logarithms with different bases. The change of base formula allows you to express any logarithm in terms of another base:
log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b)
This is particularly useful when you're working with calculators or software that only supports specific bases (like base 10 or base e). You can use this to convert all logarithms to a common base before proceeding with the solution.
Example:
log<sub>2</sub>(x) + log<sub>3</sub>(x) = 5 (This is a complex equation requiring numerical methods for precise solution)
Solution: Using the change of base formula, we can convert both to base 10 or e. This equation, however, becomes considerably more challenging to solve analytically and may require numerical methods like the Newton-Raphson method for approximation.
7. Advanced Techniques and Numerical Methods
For more complex equations involving multiple logarithms, nested logarithms, or transcendental functions alongside logarithms, analytical solutions might not always be feasible. In such cases, numerical methods become essential. These methods provide approximate solutions by iterative approaches. Common numerical methods include:
- Newton-Raphson Method: An iterative method for finding successively better approximations to the roots (or zeroes) of a real-valued function.
- Bisection Method: A root-finding method that repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing.
- Secant Method: A root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function.
These methods are typically implemented using programming languages or specialized mathematical software.
Practical Applications and Examples
Rewriting equations without logarithms finds applications in various fields:
-
Chemistry: Calculating pH values, equilibrium constants, and reaction rates often involve logarithmic relationships. Rewriting these equations can simplify calculations and provide better insight into the underlying chemical processes.
-
Physics: Many physical phenomena, such as radioactive decay, sound intensity, and stellar magnitudes, are described using logarithmic scales. Understanding how to manipulate these equations is crucial for solving problems in these areas.
-
Finance: Compound interest calculations, determining the present value of future payments, and understanding the growth of investments frequently involve logarithms. Removing logarithms can simplify these calculations.
-
Computer Science: Logarithmic time complexity in algorithms, representing data structures, and analyzing computational efficiency often involves logarithmic relationships.
-
Engineering: Various engineering disciplines use logarithmic scales for measuring signal strength, analyzing noise levels, and calculating damping factors.
Example in Finance:
The formula for compound interest with continuous compounding is:
A = Pe<sup>rt</sup>
Where:
- A = final amount
- P = principal amount
- r = annual interest rate
- t = time in years
- e = Euler's number
This equation is already free of logarithms. But if we wanted to find the time it takes to reach a specific amount A, we would need to use logarithms to solve for t:
ln(A/P) = rt
t = ln(A/P) / r
This illustrates how logarithmic and exponential forms are interconnected, and the ability to move between them is essential for problem-solving.
Conclusion
Removing logarithms from equations is a valuable skill that enhances mathematical understanding and problem-solving capabilities. The techniques outlined in this guide provide a framework for approaching various types of logarithmic equations. Remember that while analytical solutions are preferred when possible, numerical methods are powerful tools for tackling complex scenarios where analytical solutions are elusive. Mastering these techniques empowers you to effectively handle logarithmic equations across diverse applications.
Latest Posts
Latest Posts
-
How Many Pounds Is 77 Kilograms
Apr 03, 2025
-
What Is 215 Lbs In Kg
Apr 03, 2025
-
How Big Is 48 Inches In Feet
Apr 03, 2025
-
95 Mm Is How Many Inches
Apr 03, 2025
-
How Tall Is 174cm In Feet
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Rewrite The Given Equation Without Logarithms. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
