Rectangular Equation To Polar Form Converter
Greels
Mar 29, 2025 · 5 min read
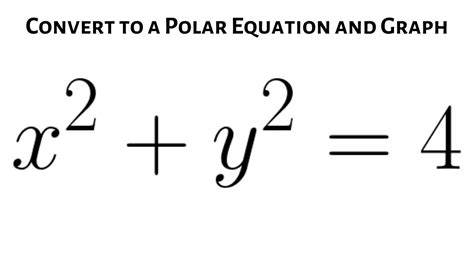
Table of Contents
Rectangular Equation to Polar Form Converter: A Comprehensive Guide
Converting equations from rectangular coordinates (x, y) to polar coordinates (r, θ) is a fundamental concept in mathematics, particularly useful in calculus, physics, and engineering. Understanding this conversion is crucial for simplifying complex equations and gaining different perspectives on geometric shapes. This comprehensive guide will walk you through the process, providing various examples and techniques for effectively converting rectangular equations to their polar counterparts.
Understanding Rectangular and Polar Coordinate Systems
Before diving into the conversion process, let's briefly review the two coordinate systems:
Rectangular Coordinates (x, y)
This is the familiar Cartesian coordinate system. A point is uniquely identified by its horizontal distance (x-coordinate) from the y-axis and its vertical distance (y-coordinate) from the x-axis.
Polar Coordinates (r, θ)
In the polar coordinate system, a point is defined by its distance (r) from the origin (called the pole) and the angle (θ) it makes with the positive x-axis. The angle θ is usually measured in radians, counter-clockwise from the positive x-axis.
The Conversion Formulas: The Heart of the Transformation
The key to converting between rectangular and polar coordinates lies in the following relationships derived from basic trigonometry:
- x = r cos θ
- y = r sin θ
- r² = x² + y²
- tan θ = y/x (Note: This equation only provides the angle in a specific quadrant; you'll need to consider the signs of x and y to determine the correct quadrant.)
These equations form the bedrock of our conversion process. We'll use them extensively in the examples below.
Step-by-Step Guide to Converting Rectangular Equations to Polar Form
The process generally involves substituting the rectangular coordinates (x and y) with their polar equivalents (r cos θ and r sin θ). Here's a step-by-step approach:
-
Identify the Rectangular Equation: Begin with the equation you want to convert, expressed in terms of x and y.
-
Substitute: Replace every instance of 'x' with 'r cos θ' and every instance of 'y' with 'r sin θ'.
-
Simplify: Use trigonometric identities and algebraic manipulation to simplify the resulting equation. Your goal is to express the equation in terms of 'r' and 'θ'. This often involves factoring out common terms or using identities like sin²θ + cos²θ = 1.
-
Solve for r (if possible): If possible, solve the equation explicitly for 'r' to express it as a function of 'θ'. This is ideal for graphing the polar equation. However, not all equations allow for this explicit solution.
-
Verify: It's always a good practice to verify your conversion by plotting a few points in both the rectangular and polar systems to ensure they align.
Examples: Illustrating the Conversion Process
Let's work through a variety of examples to solidify your understanding.
Example 1: Converting a Circle
Let's convert the rectangular equation of a circle centered at the origin with radius 'a': x² + y² = a²
-
Identify: x² + y² = a²
-
Substitute: Using r² = x² + y², we directly substitute: r² = a²
-
Simplify: Taking the square root of both sides, we get: r = a (or r = -a, but we typically consider only positive r)
Therefore, the polar equation of a circle centered at the origin with radius 'a' is simply r = a.
Example 2: Converting a Line
Let's convert the rectangular equation of a line passing through the origin with slope 'm': y = mx
-
Identify: y = mx
-
Substitute: Substitute y = r sin θ and x = r cos θ: r sin θ = m(r cos θ)
-
Simplify: Divide both sides by r (assuming r ≠ 0, which excludes the origin): sin θ = m cos θ
-
Solve for θ: Divide both sides by cos θ (assuming cos θ ≠ 0, which excludes the vertical line): tan θ = m
Therefore, the polar equation of a line passing through the origin with slope 'm' is θ = arctan(m).
Example 3: Converting a More Complex Equation
Let's convert the rectangular equation: x² - y² = 1
-
Identify: x² - y² = 1
-
Substitute: (r cos θ)² - (r sin θ)² = 1
-
Simplify: r²(cos²θ - sin²θ) = 1
-
Solve for r: r² = 1 / (cos²θ - sin²θ) = 1 / cos(2θ)
Therefore, the polar equation is r² = sec(2θ).
Example 4: A Parabola
Consider the parabola x = y².
-
Identify: x = y²
-
Substitute: r cos θ = (r sin θ)²
-
Simplify: r cos θ = r² sin²θ
-
Solve for r (excluding r=0): cos θ = r sin²θ => r = cos θ / sin²θ = cot θ csc θ
Therefore, the polar equation is r = cot θ csc θ.
Advanced Techniques and Considerations
For more complex equations, you might encounter situations where you cannot explicitly solve for 'r'. In such cases, implicit forms in terms of 'r' and 'θ' are acceptable. Furthermore, you might need to use trigonometric identities extensively to simplify the equations.
Remember to always consider the domain and range of the resulting polar equation. The angle θ might have restrictions depending on the original rectangular equation.
Applications of Rectangular to Polar Conversion
The ability to convert between rectangular and polar coordinates offers significant advantages in various fields:
-
Calculus: Polar coordinates often simplify the integration process, particularly when dealing with circular or radial symmetry. For example, calculating the area of a circle is far simpler using polar coordinates.
-
Physics: Many physical phenomena, such as projectile motion or planetary orbits, are more naturally described using polar coordinates.
-
Engineering: Polar coordinates are widely used in fields like robotics, navigation, and signal processing where angular relationships are crucial.
-
Computer Graphics: Polar coordinates play a significant role in creating various graphical patterns and shapes.
Conclusion: Mastering the Art of Coordinate Transformation
Converting rectangular equations to polar form is a powerful tool for mathematicians, scientists, and engineers. By mastering the fundamental conversion formulas and employing the techniques outlined in this guide, you can efficiently transform equations, simplifying complex problems and gaining valuable insights into their geometric representations. Remember to practice regularly with diverse examples to build confidence and proficiency in this essential mathematical skill. The more you practice, the more intuitive the process will become. And remember, the beauty of mathematics lies in its ability to provide multiple perspectives on the same problem, and this conversion offers a valuable alternative viewpoint!
Latest Posts
Latest Posts
-
What Is 94 Inches In Feet
Apr 01, 2025
-
Cuanto Es 165 Libras En Kilos
Apr 01, 2025
-
27 Mm Is How Many Inches
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Rectangular Equation To Polar Form Converter . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
