Rectangular Equation To Polar Equation Calculator
Greels
Mar 31, 2025 · 5 min read
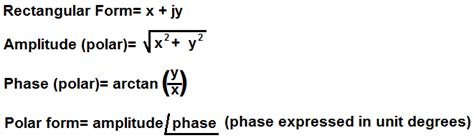
Table of Contents
Rectangular Equation to Polar Equation Calculator: A Comprehensive Guide
Converting rectangular equations to polar equations is a fundamental concept in mathematics, particularly in calculus and analytic geometry. While the process might seem daunting at first, understanding the underlying principles and utilizing the right tools can simplify the conversion significantly. This article will delve deep into the process of converting rectangular to polar equations, explore the benefits of using a rectangular equation to polar equation calculator, and provide a step-by-step guide to mastering this crucial skill. We'll also address common challenges and provide practical examples to solidify your understanding.
Understanding Rectangular and Polar Coordinate Systems
Before we jump into the conversion process, let's refresh our understanding of the two coordinate systems involved:
Rectangular Coordinates (Cartesian Coordinates)
This system, which we are most familiar with, uses two perpendicular axes, the x-axis and the y-axis, to locate a point in a plane. A point is represented by its coordinates (x, y), where x represents the horizontal distance from the origin and y represents the vertical distance from the origin.
Polar Coordinates
In the polar coordinate system, a point in a plane is represented by its distance from the origin (r) and the angle (θ) it makes with the positive x-axis. The origin is called the pole, and the positive x-axis is called the polar axis. A point is represented as (r, θ), where r ≥ 0 and 0 ≤ θ < 2π.
The Conversion Process: From Rectangular to Polar
The conversion from rectangular coordinates (x, y) to polar coordinates (r, θ) relies on the following fundamental relationships:
-
r = √(x² + y²): This equation calculates the distance (r) from the origin to the point (x, y) using the Pythagorean theorem.
-
tan(θ) = y/x: This equation calculates the angle (θ) that the line connecting the origin and the point (x, y) makes with the positive x-axis. It's crucial to consider the quadrant of the point (x, y) to determine the correct value of θ. Using the arctangent function (arctan or tan⁻¹) will give you the principal value of θ, which may need adjustment depending on the quadrant.
Converting a rectangular equation to a polar equation involves substituting these relationships into the rectangular equation. Let's illustrate this with examples:
Examples of Rectangular to Polar Equation Conversion
Example 1: Converting x² + y² = r²
This is a fundamental relationship and a straightforward example. Since r² = x² + y², the rectangular equation x² + y² = 25 directly converts to the polar equation r² = 25, which simplifies to r = 5 (since r must be non-negative). This represents a circle with a radius of 5 centered at the origin.
Example 2: Converting y = x
Here, we substitute the relationships:
- x = r cos(θ)
- y = r sin(θ)
The equation becomes: r sin(θ) = r cos(θ)
If r ≠ 0, we can divide both sides by r:
sin(θ) = cos(θ)
This simplifies to tan(θ) = 1, which means θ = π/4 or θ = 5π/4. This represents two lines passing through the origin. Note that if r = 0 we recover the origin, (0,0), which is also consistent.
Example 3: Converting x² - y² = 4
Substituting the relationships, we get:
(r cos(θ))² - (r sin(θ))² = 4
r²(cos²(θ) - sin²(θ)) = 4
Using a trigonometric identity, cos²(θ) - sin²(θ) = cos(2θ), the equation becomes:
r² cos(2θ) = 4
r² = 4 sec(2θ)
This represents a hyperbola.
The Role of a Rectangular Equation to Polar Equation Calculator
While the manual conversion process is educational and helps build a strong understanding of the underlying principles, using a rectangular equation to polar equation calculator can significantly expedite the process, especially for complex equations. Calculators can handle intricate trigonometric manipulations and algebraic simplifications efficiently, minimizing the chances of errors. They are especially valuable when dealing with equations involving higher-order polynomials or complex trigonometric functions.
Benefits of Using a Calculator:
- Speed and Efficiency: Calculators perform conversions much faster than manual calculations.
- Accuracy: Reduces the risk of human error during algebraic manipulations and trigonometric calculations.
- Handling Complex Equations: Calculators can tackle equations that are difficult or time-consuming to solve manually.
- Learning Tool: Using a calculator alongside manual calculations provides opportunities to check your work and learn from any discrepancies.
Choosing the Right Calculator
When choosing a rectangular equation to polar equation calculator, consider the following:
- Ease of Use: The interface should be intuitive and user-friendly.
- Accuracy: The calculator should provide accurate results.
- Functionality: Consider additional features such as graphing capabilities or the ability to handle different types of equations.
- Availability: Choose a calculator that's easily accessible—online calculators are often convenient.
Common Challenges and Troubleshooting
Converting rectangular equations to polar equations can present several challenges:
- Dealing with Trigonometric Identities: Recognizing and applying relevant trigonometric identities is crucial for simplification.
- Handling Multiple Solutions: Some equations may have multiple solutions for θ, requiring careful consideration of the quadrants.
- Dealing with Undefined Values: Pay attention to cases where expressions might be undefined (e.g., division by zero).
Advanced Applications
The conversion between rectangular and polar equations has several advanced applications:
- Calculus: Polar coordinates are often preferred for calculating areas and volumes of regions with circular or radial symmetry.
- Physics and Engineering: Polar coordinates are widely used in fields like mechanics, electromagnetism, and fluid dynamics.
- Computer Graphics: The conversion is essential for rendering graphics and working with shapes in computer-aided design (CAD) software.
- Signal Processing: Polar coordinates are used to analyze signals in frequency domain.
Conclusion
Converting rectangular equations to polar equations is a critical skill in mathematics and various scientific and engineering disciplines. While mastering the manual conversion process is essential for a deeper understanding, utilizing a rectangular equation to polar equation calculator significantly enhances efficiency and accuracy, especially when dealing with complex equations. By understanding the principles, employing the right tools, and addressing common challenges, you can confidently navigate this important mathematical transformation. Remember to always verify your results and utilize additional resources to reinforce your learning. The ability to seamlessly convert between these coordinate systems opens doors to a more profound understanding of mathematical concepts and their applications in diverse fields.
Latest Posts
Latest Posts
-
Cuanto Es 172 Libras En Kilos
Apr 02, 2025
-
How Many Inches Is 0 55 Feet
Apr 02, 2025
-
How Much Is 300 Miles In Kilometers
Apr 02, 2025
-
How Many Feet Is 35 In
Apr 02, 2025
-
How Long Is 100 Cm In Feet
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Rectangular Equation To Polar Equation Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
