Pr 9x 31 And Qr 43 Find X
Greels
Apr 01, 2025 · 5 min read
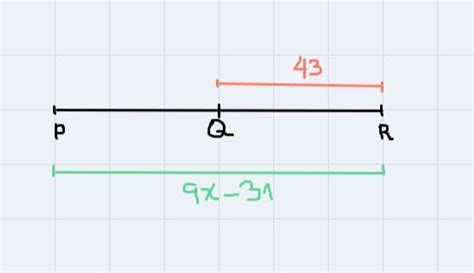
Table of Contents
Solving for x: A Deep Dive into PR 9x + 31 and QR 43
This article will explore the mathematical problem of solving for 'x' in equations involving trigonometric functions, specifically focusing on scenarios where we encounter expressions like PR 9x + 31 and QR 43. While the notations "PR" and "QR" aren't standard mathematical conventions, we'll interpret them as representing some form of relationship or equation involving 'x'. We'll examine various approaches to tackle such problems, emphasizing the importance of understanding fundamental trigonometric identities and algebraic manipulation. This will be a comprehensive guide, exploring multiple scenarios and highlighting potential pitfalls.
Understanding the Problem's Structure
Before delving into specific solutions, let's dissect the core components of the problem. We're presented with two expressions: PR 9x + 31 and QR 43. The crucial element is the variable 'x', which we need to isolate and solve for. The challenge lies in the potentially complex relationship between 'x' and the trigonometric functions implied by "PR" and "QR". We must carefully interpret these notations and apply the appropriate mathematical techniques.
We'll consider several possibilities to demonstrate a flexible approach.
Scenario 1: Interpreting "PR" and "QR" as Trigonometric Functions
Let's assume "PR" and "QR" represent trigonometric functions like sine, cosine, or tangent. We can reframe the problem in a more conventional mathematical format. For example, let's say:
- PR represents the sine function: sin(9x + 31)
- QR represents the cosine function: cos(43)
Now our problem becomes:
sin(9x + 31) = cos(43)
To solve this, we'll use trigonometric identities to manipulate the equation and isolate 'x'. Recall the cofunction identity:
sin(θ) = cos(90° - θ)
Applying this identity, we can rewrite the equation as:
cos(90° - (9x + 31)) = cos(43)
This simplifies to:
cos(59 - 9x) = cos(43)
Because the cosine function is periodic, there are multiple solutions. The general solution for cos(A) = cos(B) is:
A = ±B + 2nπ (where n is an integer)
Substituting our expressions, we get:
59 - 9x = ±43 + 2nπ
Now we have two separate equations to solve for x:
- 59 - 9x = 43 + 2nπ
- 59 - 9x = -43 + 2nπ
Solving for x in each equation:
- 9x = 16 - 2nπ => x = (16 - 2nπ) / 9
- 9x = 102 - 2nπ => x = (102 - 2nπ) / 9
These equations give us an infinite set of solutions for x, depending on the integer value of 'n'.
Scenario 2: "PR" and "QR" Represent Linear Equations
Alternatively, if "PR" and "QR" represent linear equations, our problem might take a different form. Let's assume:
- PR implies a linear equation: y = 9x + 31
- QR implies a linear equation: y = 43
Now, we're solving:
9x + 31 = 43
Solving for x is straightforward:
9x = 12
x = 12/9 = 4/3
In this scenario, we have a single, unique solution for x.
Scenario 3: "PR" and "QR" Representing Geometric Relationships
We could also interpret "PR" and "QR" as representing lengths in a geometric context. For instance, they might be sides of a triangle, where trigonometric functions become relevant. Without specific details about the geometric configuration, we cannot offer a concrete solution. However, the approach would involve applying geometric theorems and trigonometric identities to establish a relationship between the lengths and angle 'x'.
Importance of Context and Clarity in Mathematical Notation
The ambiguity in the original problem highlights the critical importance of precise mathematical notation. The use of non-standard symbols like "PR" and "QR" obscures the underlying mathematical relationship and makes it challenging to find a unique solution. For effective communication and problem-solving, it is essential to use standardized notation and clearly define the context of the variables and equations.
Advanced Techniques and Considerations
This problem, even with clarified notations, could involve more advanced techniques depending on the specific interpretation. These might include:
-
Inverse Trigonometric Functions: If trigonometric functions are involved, using inverse functions (arcsin, arccos, arctan) is crucial to isolate x. Remember that inverse trigonometric functions often have multiple solutions (due to periodicity), requiring careful consideration of the range of possible values for x.
-
Numerical Methods: If an analytical solution is intractable, numerical methods like the Newton-Raphson method might be used to approximate the solution for x.
-
Calculus: In more complex scenarios involving curves or rates of change, calculus could become necessary to solve for x.
-
Complex Numbers: Depending on the functions involved, the solution for x might involve complex numbers.
Practical Applications and Real-World Examples
The ability to solve equations involving trigonometric functions and algebraic manipulation has vast applications across numerous fields:
-
Engineering: Solving for unknown angles or distances in structural design, mechanics, or electrical circuits.
-
Physics: Analyzing projectile motion, wave phenomena, or oscillatory systems.
-
Computer Graphics: Modeling 3D shapes and transformations, rendering realistic images.
-
Navigation: Determining distances and bearings using triangulation or other techniques.
Conclusion
Solving for 'x' in equations involving expressions like PR 9x + 31 and QR 43 requires a clear understanding of the underlying mathematical relationships. The ambiguity of the notation "PR" and "QR" necessitates careful interpretation and consideration of various scenarios. This article has provided several potential interpretations, showcasing diverse problem-solving approaches and highlighting the importance of precision in mathematical communication. Remember to always define your variables and functions explicitly, utilizing standard mathematical notation for clarity and accuracy in your work. By mastering these techniques, you'll enhance your problem-solving skills and unlock the power of mathematics in diverse fields.
Latest Posts
Latest Posts
-
185 Pounds Is How Many Kg
Apr 02, 2025
-
100 Ft Equals How Many Meters
Apr 02, 2025
-
How Many Inches In 105 Cm
Apr 02, 2025
-
How Many Cm Is 76 Inches
Apr 02, 2025
-
How Many Inches In 71 Cm
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Pr 9x 31 And Qr 43 Find X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
