Integral Of 1 Y 1 2
Greels
Mar 29, 2025 · 5 min read
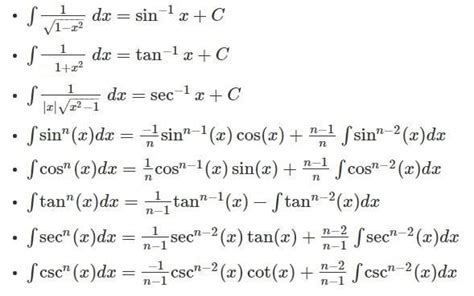
Table of Contents
Understanding and Solving the Integral of 1/(y^2 + 1)
The integral ∫1/(y² + 1) dy is a fundamental integral in calculus, frequently encountered in various applications. Its solution is a crucial building block for understanding more complex integration techniques and solving problems in fields like physics, engineering, and statistics. This comprehensive guide will delve into the intricacies of solving this integral, exploring its derivation, applications, and related concepts.
The Significance of the Integral ∫1/(y² + 1) dy
This particular integral is significant for several reasons:
-
Simplicity and Elegance: Despite its seemingly simple form, the integral reveals a powerful connection between trigonometric functions and their inverses. The solution elegantly illustrates the relationship between differentiation and integration.
-
Foundation for More Complex Integrals: Understanding this integral is a cornerstone for tackling more complex integrals involving rational functions, particularly those involving quadratic expressions in the denominator. Techniques like partial fraction decomposition often rely on recognizing and handling integrals similar to this one.
-
Wide Applicability: The integral appears in numerous applications, including the calculation of areas under curves, volumes of solids of revolution, and solutions to differential equations that model various physical phenomena.
Solving the Integral: The Arctangent Function
The solution to the integral ∫1/(y² + 1) dy is the arctangent function, denoted as arctan(y) or tan⁻¹(y). This function is the inverse of the tangent function.
Derivation:
While a rigorous proof involving trigonometric substitution is possible, a simpler approach relies on recognizing the derivative of arctan(y):
-
Recall: The derivative of arctan(y) with respect to y is given by: d/dy [arctan(y)] = 1/(y² + 1)
-
Integration as the Reverse of Differentiation: Since integration is the reverse process of differentiation, it follows directly that the integral of 1/(y² + 1) with respect to y is arctan(y):
∫1/(y² + 1) dy = arctan(y) + C
Where 'C' represents the constant of integration. This constant is crucial because the derivative of any constant is zero. Therefore, an infinite number of functions could have 1/(y² + 1) as their derivative. The constant of integration accounts for this ambiguity.
Trigonometric Substitution: A More Formal Approach
A formal derivation utilizes trigonometric substitution. Let's substitute y = tan(θ). Then, dy = sec²(θ)dθ. Substituting these into the integral:
∫1/(y² + 1) dy = ∫1/(tan²(θ) + 1) sec²(θ)dθ
Using the trigonometric identity tan²(θ) + 1 = sec²(θ), the integral simplifies to:
∫1/sec²(θ) sec²(θ)dθ = ∫1 dθ = θ + C
Since y = tan(θ), we can express θ as arctan(y). Substituting this back into the equation, we obtain:
θ + C = arctan(y) + C
This confirms the result obtained earlier.
Applications of the Arctangent Integral
The arctangent function, and therefore the integral ∫1/(y² + 1) dy, finds application in a wide range of fields:
1. Calculus and Analysis:
-
Calculating Areas: The integral can compute the area under the curve 1/(y² + 1) between specific limits. This area has geometric significance and relates to the arctangent function's properties.
-
Evaluating Definite Integrals: The integral is essential in evaluating definite integrals involving the function 1/(y² + 1), which are often encountered in problems concerning probability and statistics.
-
Solving Differential Equations: The integral appears as a solution in several types of differential equations, especially those involving separable variables or integrable combinations.
2. Physics and Engineering:
-
Electromagnetism: Arctangent functions are used extensively in electromagnetism calculations, particularly those related to electric and magnetic fields. The integral plays a role in analyzing field distributions and potentials.
-
Fluid Mechanics: In fluid dynamics, the arctangent function can appear in solutions for fluid flow problems, particularly those involving potential flow or boundary layer analysis.
-
Signal Processing: The arctangent function has applications in signal processing, particularly in phase detection and signal demodulation.
3. Statistics and Probability:
-
Probability Distributions: The arctangent function is related to certain probability distributions, such as the Cauchy distribution. The integral helps calculate probabilities associated with these distributions.
-
Statistical Inference: In statistical inference, the arctangent transformation can be used to stabilize variances and improve the normality of data.
4. Computer Graphics and Game Development:
-
Rotation and Orientation: Arctangent functions are fundamental to calculating angles and rotations in 2D and 3D graphics and game development. They are essential for representing object orientation and manipulating camera views.
-
Inverse Kinematics: In robotics and animation, inverse kinematics uses arctangent functions to determine joint angles required to achieve a desired end-effector position.
Generalizations and Extensions
The integral ∫1/(y² + 1) dy is a fundamental case. Understanding it helps solve more generalized forms:
1. Integrals of the form ∫1/(x² + a²) dx:
This integral can be solved using a simple substitution. Let u = x/a. Then du = dx/a, and x = au. The integral becomes:
∫1/(a²(u² + 1)) * a du = (1/a) ∫1/(u² + 1) du = (1/a) arctan(u) + C = (1/a) arctan(x/a) + C
2. Integrals with shifted denominators:
Integrals of the form ∫1/((x-a)² + b²) dx can be solved using a similar substitution, transforming it into the standard arctangent integral form. The key is to manipulate the expression in the denominator to resemble (u² + 1).
3. Integrals involving more complex rational functions:
Many more complex integrals involving rational functions can be solved using partial fraction decomposition. This technique breaks down complex fractions into simpler forms, some of which might involve integrals similar to ∫1/(y² + 1) dy.
Conclusion
The integral ∫1/(y² + 1) dy, which evaluates to arctan(y) + C, is a cornerstone of integral calculus. Its elegant solution showcases the powerful relationship between differentiation and integration, and its wide-ranging applications across numerous disciplines highlight its fundamental importance. By thoroughly understanding this integral and the related concepts discussed, you'll gain a stronger foundation for tackling more complex integration problems and solving a broader range of mathematical and scientific challenges. The constant of integration, often overlooked, emphasizes the importance of understanding the family of functions that share the same derivative. Mastering this integral provides a crucial stepping stone for advanced mathematical explorations.
Latest Posts
Latest Posts
-
What Is 75 Inches In Cm
Apr 01, 2025
-
What Is 94 Inches In Feet
Apr 01, 2025
-
Cuanto Es 165 Libras En Kilos
Apr 01, 2025
-
27 Mm Is How Many Inches
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 Y 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
